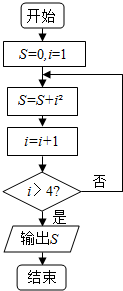
题目内容
16.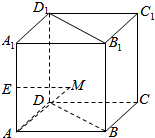 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是线段AA1的中点,M是平面BB1D1D内的点,则|AM|+|ME|的最小值是$\frac{3}{2}$;若|ME|≤1,则点M在平面BB1D1D内形成的轨迹的面积等于$\frac{π}{2}$.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是线段AA1的中点,M是平面BB1D1D内的点,则|AM|+|ME|的最小值是$\frac{3}{2}$;若|ME|≤1,则点M在平面BB1D1D内形成的轨迹的面积等于$\frac{π}{2}$.
分析 (1)由图形可知AC⊥平面BB1D1D,且A到平面BB1D1D的距离与C到平面BB1D1D的距离相等,故MA=MC,所以EC就是|AM|+|ME|的最小值;
(2)设点E在平面BB1D1D的射影为O,则EO=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,令ME=1,则△EMO是直角三角形,所以点M在平面BB1D1D上的轨迹为圆,有勾股定理求得OM=$\frac{\sqrt{2}}{2}$,即点M的轨迹半径为$\frac{\sqrt{2}}{2}$,代入圆面积公式即可求得面积.
解答 解:连接AC交BD于N,连接MN,MC,
则AC⊥BD,
∵BB1⊥平面ABCD,
∴BB1⊥AC,
∴AC⊥平面BB1D1D,
∴AC⊥MN,
∴△AMN≌△CMN,
∴MA=MC,
连接EC,
∴线段EC的长就是|AM|+|ME|的最小值.
在Rt△EAC中,AC=$\sqrt{2}$,EA=$\frac{1}{2}$,∴EC=$\sqrt{A{C}^{2}+E{A}^{2}}$=$\frac{3}{2}$.
过E作平面BB1D1D的垂线,垂足为O,则EO=AN=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,
令EM=1,则M的轨迹是以O为圆心,以OM为半径的圆,
∴OM=$\sqrt{E{M}^{2}-E{O}^{2}}$=$\frac{\sqrt{2}}{2}$,
∴S=π•($\frac{\sqrt{2}}{2}$)2=$\frac{π}{2}$.
故答案为$\frac{3}{2}$,$\frac{π}{2}$
点评 本题考查了空间几何中的最值问题,找到MA与MC的相等关系是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列判断正确的是( )
| A. | 函数f(x)=1既是奇函数又是偶函数 | B. | 函数f(x)=(1-x)$\sqrt{\frac{1+x}{1-x}}$是偶函数 | ||
| C. | 函数f(x)=$\frac{{x}^{2}-2x}{x-2}$是奇函数 | D. | 函数f(x)=x+$\sqrt{{x}^{2}-1}$是非奇非偶函数 |