题目内容
12.已知函数f(x)=ax3+2x-a,(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若a=n且n∈N*,设xn是函数fn(x)=nx3+2x-n的零点.
(i)证明:n≥2时存在唯一xn且${x}_{n}∈(\frac{n}{n+1},1)$;
(i i)若bn=(1-xn)(1-xn+1),记Sn=b1+b2+…+bn,证明:Sn<1.
分析 (Ⅰ)对f(x)求导得到单调区间
(Ⅱ)(i)由(Ⅰ)得,fn(x)=nx3+2x-n在R上单调递增,证明fn($\frac{n}{n+1}$)=-$(\frac{n}{n+1})^{3}(\frac{{n}^{2}-n-1}{{n}^{2}})$即可.
(ii)利用数列裂项求和和不等式放缩技巧证明即可.
解答 解:(Ⅰ)f'(x)=3ax2+2,
若a≥0,则f'(x)>0,函数f(x)在R上单调递增;
若a<0,令f'(x)>0,∴$x>\sqrt{\frac{2}{3a}}$或$x<-\sqrt{\frac{2}{3a}}$,
函数f(x)的单调递增区间为$(-∞,\sqrt{\frac{2}{3a}})$和$(\sqrt{\frac{2}{3a}},+∞)$;
(Ⅱ)(i)由(Ⅰ)得,fn(x)=nx3+2x-n在R上单调递增,
又fn(1)=n+2-n=2>0,
fn($\frac{n}{n+1}$)=$n(\frac{n}{n+1})^{3}+2(\frac{n}{n+1})-n$=$n(\frac{n}{n+1})^{3}+2(\frac{n}{n+1})-n$
=$(\frac{n}{n+1})^{3}(n+\frac{2(n+1)^{2}}{{n}^{2}}\frac{(n+1)^{3}}{{n}^{2}})$=-$(\frac{n}{n+1})^{3}(\frac{{n}^{2}-n-1}{{n}^{2}})$
当n≥2时,g(n)=n2-n-1>0,${f}_{n}(\frac{n}{n+1})<0$,
n≥2时存在唯一xn且${x}_{n}∈(\frac{n}{n+1},1)$
(i i)当n≥2时,${x}_{n}∈(\frac{n}{n+1},1)$,∴$0<1-{x}_{n}<\frac{1}{n+1}$(零点的区间判定)
∴${b}_{n}<\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,(数列裂项求和)
∴${S}_{n}={b}_{1}+{b}_{2}+…+{b}_{n}<{b}_{1}+\frac{1}{3}-\frac{1}{n+1}$,
又f1(x)=x3+2x-1,${f}_{1}(\frac{1}{3})=-\frac{8}{27}<0,{f}_{1}(\frac{2}{3})=\frac{17}{27}>0$,(函数法定界)
$\frac{1}{3}<1-{x}_{1}<\frac{2}{3}$,又$0<1-{x}_{2}<\frac{1}{3}$,
∴$0<(1-{x}_{1})(1-{x}_{2})<\frac{2}{9}$,
∴${S}_{n}={b}_{1}+{b}_{2}+…+{b}_{n}<\frac{2}{9}$$+\frac{1}{3}-\frac{1}{n+1}<1-\frac{1}{n+1}<1$,(不等式放缩技巧)
命题得证.
点评 本题主要考查了导数的求单调区间的方法和利用数列的裂项求和和不等式的放缩求和技巧解题,属于难题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案| A. | 15π | B. | $\frac{15π}{4}$ | C. | $\sqrt{15}$ π | D. | 6π |
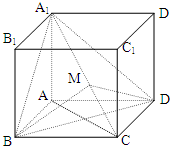 如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.