题目内容
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,以椭圆上任一点与左,右焦点F1,F2为顶点的三角形的周长为4($\sqrt{2}$+1).(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线l1过原点O,直线l2与直线l1相交于点Q,|$\overrightarrow{OQ}$|=1,且l2⊥l1,直线l2与椭圆交于A,B两点,问是否存在这样的直线l2,使$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1成立.若存在,求出直线l2的方程;若不存在,请说明理由.
分析 (Ⅰ)由题意,得2a+2c=4($\sqrt{2}$+1),$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,求出a,b,c,即可求椭圆的标准方程;
(2)分类讨论,根据$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1,|$\overrightarrow{OQ}$|=1进行转化,将直线l2的方程为mx+ny=1代入椭圆方程,利用x1x2+y1y2=0,即可得出结论.
解答 解:(Ⅰ)由题意,得2a+2c=4($\sqrt{2}$+1),$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,…(2分)
∴a=2$\sqrt{2}$c=2,b=2.
∴椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$. …(4分)
(Ⅱ)假设存在直线l2,使$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1成立.
设A,B两点的坐标分别为(x1,y1),(x2,y2),Q(m,n),且m2+n2=1,
则直线l1的方程为nx-my=0,直线l2的方程为mx+ny=1.
(1)当n=0时,此时直线l2的方程为x=±1,可得A(1,$\frac{\sqrt{14}}{2}$),B(1,-$\frac{\sqrt{14}}{2}$),
代入$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1,不符题意; …(5分)
(2)当n≠0时,将直线l2的方程为mx+ny=1与椭圆方程$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$联立,
又m2+n2=1,得 (1+m2)x2-4mx+2-8n2=0. …(6分)
∴x1+x2=$\frac{4m}{1+{m}^{2}}$,x1x2=$\frac{2-8{n}^{2}}{1+{m}^{2}}$. …(7分)
又∵$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1,
∴x1x2+y1y2+2=m(x1+x2)+n(y1+y2).
又 mx1+ny1=1,mx2+ny2=1
∴m(x1+x2)+n(y1+y2)=2.
∴x1x2+y1y2=0. …(9分)
∴n2x1x2+1+m2x1x2-m(x1+x2)=0.
∴x1x2+1-m(x1+x2)=0. …(11分)
∴-5n2=0.
∴n=0这与n≠0矛盾. …(12分)
综上可知,不存在这样的直线l2,使$\overrightarrow{AQ}$•$\overrightarrow{BQ}$=-1成立. …(13分)
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案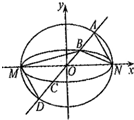 如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.
如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.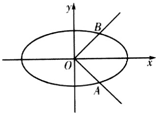 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.