题目内容
【题目】已知椭圆 ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4
,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4 ![]() .
. 
(1)求椭圆的方程;
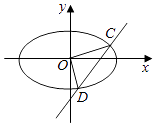
(2)如图,直线x=ty+m交椭圆于不同两点C,D,若以线段CD为直径的圆过原点O,求|CD|的取值范围.
【答案】
(1)解:由椭圆的定义可得|AF1|+|AF2|=|BF1|+|BF2|=2a,
即有△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|AF2|+|BF1|+|BF2|=4a=4 ![]() ,可得a=
,可得a= ![]() ,
,
e= ![]() =
= ![]() ,可得c=2,b=
,可得c=2,b= ![]() =1,
=1,
即有椭圆的方程为 ![]() +y2=1
+y2=1
(2)解:当直线OC的斜率不存在或斜率为0时,
可得|CD|= ![]() =
= ![]() ,
,
当直线OC的斜率存在时,
设直线OC的方程为y=kx(k≠0),直线OD的方程为:y=﹣ ![]() x
x
联立 ![]() ,解得x2=
,解得x2= ![]() ,y2=
,y2= ![]() .
.
∴|OC|2=x2+y2= ![]() .
.
同理可得|OD|2= ![]() .
.
∴|CD|2=|OC|2+|OD|2= ![]() +
+ ![]() =
= ![]()
= 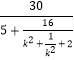 ≥
≥ ![]() ,当k2=1时取等号.
,当k2=1时取等号.
∴|CD|≥ ![]() .
.
综上可得, ![]() ≤|CD|≤
≤|CD|≤ ![]()
【解析】(2)当直线OC的斜率不存在或斜率为0时,可得|CD|= ![]() =
= ![]() .当直线OC的斜率存在时,设直线OC的方程为y=kx(k≠0),直线OD的方程为:y=﹣
.当直线OC的斜率存在时,设直线OC的方程为y=kx(k≠0),直线OD的方程为:y=﹣ ![]() x联立椭圆方程,解得x2 , y2 . 可得|OC|2=x2+y2=
x联立椭圆方程,解得x2 , y2 . 可得|OC|2=x2+y2= ![]() .同理可得|OD|2=
.同理可得|OD|2= ![]() .可得|CD|2=|OC|2+|OD|2 , 求得最小值,即可得出范围.
.可得|CD|2=|OC|2+|OD|2 , 求得最小值,即可得出范围.

【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
参考公式:线性回归方程 ![]() ,其中
,其中  .
.
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?