题目内容
【题目】已知函数f(x)=ax2+8x+b(a,b为互不相等的正整数),方程f(x)=0的两个实根为x1 , x2(x1≠x2),且|x1|<1,|x2|<1,若f(1)+f(﹣1)的最大值与最小值分别为M,m,则M+m的值为 .
【答案】50
【解析】解:f(x)=ax2+8x+b,
此函数的图象与x轴的两个交点在区间(﹣1,1),
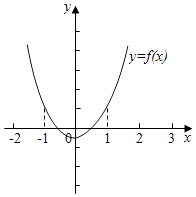
∴ 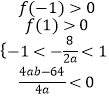
∴  即有
即有 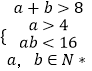 ,
,
∵a,b为互不相等的正整数,
∴a,b可能的取值有(7,2)(8,1)(9,1)(10,1),
(11,1),(12,1),(13,1),(14,1)(15,1)共9个.
∴a+b的最小值是9,最大值为16.
则f(1)+f(﹣1)=2(a+b)的最大值与最小值分别为M=32,m=18,
可得M+m=50.
故答案为:50.
由|x1|<1,|x2|<1知,方程的两根在区间(﹣1,1)内,f(x)=ax2+8x+b,此函数的图象与x轴的两个交点在区间(﹣1,1)内,可得,f(﹣1)>0,f(1)>0,且对称轴在区间(﹣1,1)内,最小值小于0.由此列条件求a+b的最值,进而得到M+m的和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目