题目内容
17.在△ABC中,B=30°,BC=20,AC=11,则cosA的值是$±\frac{\sqrt{21}}{11}$.分析 利用已知及余弦定理先求AB的值,再利用余弦定理即可求得cosA的值.
解答 解:∵B=30°,BC=20,AC=11,
∴由余弦定理AC2=AB2+BC2-2AB•AC•cosB可得:112=202+AB2-2×20×AB×cos30°,
∴整理可得:AB2-20$\sqrt{3}$AB+279=0,解得:AB=10$\sqrt{3}$±$\sqrt{21}$,
∴由余弦定理可得:cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{(10\sqrt{3}±\sqrt{21})^{2}+1{1}^{2}-2{0}^{2}}{2×(10\sqrt{3}±\sqrt{21})×11}$=$±\frac{\sqrt{21}}{11}$.
故答案为:$±\frac{\sqrt{21}}{11}$.
点评 本题主要考查了余弦定理的应用,考查了计算能力,属于基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若以C的焦点F为圆心a为半径的圆,截双曲线的渐近线所得弦长为b,则此双曲线的离心率是( )
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
12.在△ABC中,a=3$\sqrt{3}$,b=2,cosC=$-\frac{{\sqrt{3}}}{2}$,则c等于( )
| A. | 13 | B. | $\sqrt{13}$ | C. | 7 | D. | 9 |
2.某人射击命中目标的概率为0.6,每次射击互不影响,连续射击3次,至少有2次命中目标的概率为( )
| A. | $\frac{84}{125}$ | B. | $\frac{81}{125}$ | C. | $\frac{36}{125}$ | D. | $\frac{27}{125}$ |
15.在△ABC中,D为BC边中点,O为△ABC内一点,且$\overrightarrow{OC}$=2$\overrightarrow{AO}$+$\overrightarrow{BO}$,则$\frac{{S}_{△AOC}}{{S}_{△BOD}}$=( )
| A. | $\frac{5}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 1 |
16.已知直线l1:x+2y-5=0,l2:2x+y+2=0,则直线l1与直线l2及x轴所围成的三角形的面积是( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
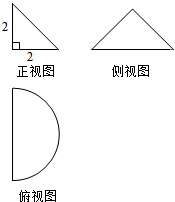 一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积为4+2π+2$\sqrt{2}$π.体积分别为$\frac{4}{3}$π.
一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积为4+2π+2$\sqrt{2}$π.体积分别为$\frac{4}{3}$π.