题目内容
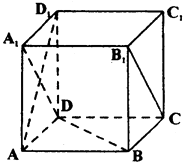
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是正方体棱上的一点(不包括棱的端点),满足|PB|+|PD1|= ![]() 的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
【答案】12;(2 ![]() ,2
,2 ![]() )
)
【解析】解:∵正方体的棱长为2,
∴BD1= ![]() =2
=2 ![]() ,
,
∵点P是正方体棱上的一点(不包括棱的端点),满足|PB|+|PD1|= ![]() ,
,
∴点P是以2c=2 ![]() 为焦距,以a=
为焦距,以a= ![]() 为长半轴,以
为长半轴,以 ![]() 为短半轴的椭圆,
为短半轴的椭圆,
∵P在正方体的棱上,
∴P应是椭圆与正方体与棱的交点,
结合正方体的性质可知,满足条件的点应该在正方体的12条棱上各有一点满足条件.
∴满足|PB|+|PD1|= ![]() 的点P的个数为12个.(2)∵满足|PB|+|PD1|=m的点P的个数为6,
的点P的个数为12个.(2)∵满足|PB|+|PD1|=m的点P的个数为6,
∴|PB|+|PD1|=m>|BD1|=2 ![]() ,∴m>2
,∴m>2 ![]() ,
,
∵正方体的棱长为2,∴正方体的面的对角线的长为2 ![]() ,
,
∵点P的个数为6,∴b< ![]() ,
,
∵短半轴长b= ![]() ,∴
,∴ ![]()
![]() ,解得m<2
,解得m<2 ![]() .
.
∴m的取值范围是(2 ![]() ,2
,2 ![]() ).
).
所以答案是:12,(2 ![]() ,2
,2 ![]() ).
).

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
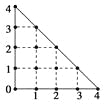
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.