题目内容
【题目】(1)已知
，用分析法证明: 
；
(2)已知
， 
且
，用反证法证明: 
都大于零．
【答案】(1) 见解析(2) 见解析
【解析】试题分析：（1）用分析法证明, 
…
；（2）假设
不都大于零，即至少有一个小于零或等于零，这时需要逐个讨论
不是正数的情形.但注意到条件的特点（任意交换
的位置不改变命题的条件），我们只要讨论其中一个数（例如
），其他两个数（例如
）与这种情形类似.
试题解析：(1)因为
欲使
由已知得最后一个不等式成立，
故原不等式成立；
(2) 假设
不都大于零，即至少有一个小于零或等于零
(ⅰ) 若某一个等于零，由
，与
矛盾．
(ⅱ) 若某一个小于零，不妨设
，由
，得
由
，得
，那么
，得
，
即
，结合
，得
与
矛盾．
结合(1)、(2) 知
都大于零．
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据．
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）请根据上表提供的数据，用最小二乘法求出y关于x的回归方程 
= 
x+ 
；
（2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（1）求出的回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？ （参考数值：3×2.5+4×3+5×4+6×4.5=66.5）计算回归系数 ， ．公式为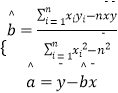 
．
