题目内容
【题目】已知数列{an}中, ![]() (Ⅰ)求证:
(Ⅰ)求证: ![]() 是等比数列,并求{an}的通项公式an;
是等比数列,并求{an}的通项公式an;
(Ⅱ)数列{bn}满足 ![]() ,数列{bn}的前n项和为Tn , 若不等式
,数列{bn}的前n项和为Tn , 若不等式 ![]() 对一切n∈N*恒成立,求λ的取值范围.
对一切n∈N*恒成立,求λ的取值范围.
【答案】证明:(Ⅰ)由 ![]() ,得
,得 ![]() =
= ![]() =1+
=1+ ![]() , 即
, 即 ![]() +1=2(
+1=2( ![]() ),
),
又 ![]() ,∴
,∴  是以2为首项,2为公比的等比数列.
是以2为首项,2为公比的等比数列.
∴ ![]() +1=2×2n﹣1=2n , 即
+1=2×2n﹣1=2n , 即 ![]() .
.
解:(Ⅱ)bn= ![]() ,
,
Tn=1× ![]() +…+(n﹣1)×
+…+(n﹣1)× ![]() ,
,![]() =
= ![]() ,
,
两式相减得:![]() =
= ![]() ﹣n×
﹣n× ![]() =2﹣
=2﹣ ![]() ,
,
Tn=4﹣ ![]() ,
,
∴(﹣1)nλ<4﹣ ![]() ,
,
令Sn=4﹣ ![]() ,由题意知Sn单调递增.
,由题意知Sn单调递增.
若n为偶数,则λ<4﹣ ![]() ,Sn|min=S2=3,
,Sn|min=S2=3,
∴λ<3.
若n为奇数,则﹣λ<4﹣ ![]() ,Sn|min=S1=2,
,Sn|min=S1=2,
∴﹣λ<2,∴λ>﹣2,
∴﹣2<λ<3.即λ的取值范围是(﹣2,3).
【解析】(Ⅰ)由 ![]() ,得
,得 ![]() +1=2(
+1=2( ![]() ),由此能证明
),由此能证明 ![]() 是以2为首项,2为公比的等比数列,并能求出{an}的通项公式an . (Ⅱ)由bn=
是以2为首项,2为公比的等比数列,并能求出{an}的通项公式an . (Ⅱ)由bn= ![]() ,利用错位相减法能求出Tn=4﹣
,利用错位相减法能求出Tn=4﹣ ![]() ,从而(﹣1)nλ<4﹣
,从而(﹣1)nλ<4﹣ ![]() ,由此能求出λ的取值范围.
,由此能求出λ的取值范围.
【考点精析】认真审题,首先需要了解等比数列的通项公式(及其变式)(通项公式:![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 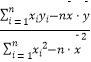 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.
