题目内容
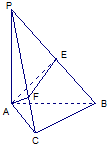
如图,矩形ABCD中,BC=2,AB=1,PA丄平面ABCD,BE∥PA,BE=
PA,F为PA的中点.
(I)求证:DF∥平面PEC
(II)若PE=
,求平面PEC与平面PAD所成锐二面角的余弦值.

| 1 |
| 2 |
(I)求证:DF∥平面PEC
(II)若PE=
| 2 |

(Ⅰ)证明:理解EF,∵BE∥PA,BE=
PA=AF,∴四边形ABEF是平行四边形.
∴EF
BA,
∵矩形ABCD,∴BA
CD.
∴EF
CD.
∴四边形EFDC是平行四边形.
∴DF∥CE.
∵DF?平面PEC,EC?平面PEC.
∴DF∥平面PEC.
(Ⅱ)∵AP⊥平面ABCD,四边形ABCD为矩形,
以点A为坐标原点,建立如图所示的空间直角坐标系A-xyz.
在Rt△PEF中,PE=
,EF=AB=1,∴PF=1.
可得P(0,0,2),E(1,0,1),C(1,2,0),
∴
=(1,0,-1),
=(1,2,-2).
设平面PEC的法向量为
=(x,y,z).
则
,得
,
令x=2,则z=2,y=1,∴
=(2,1,2).
∵AB⊥平面PAD,∴可取
=(1,0,0)作为平面PAD的法向量.
∴cos<
,
>=
=
=
.
故平面PEC与平面PAD所成锐二面角的余弦值为
.
| 1 |
| 2 |

∴EF
| ∥ |
| . |
∵矩形ABCD,∴BA
| ∥ |
| . |
∴EF
| ∥ |
| . |
∴四边形EFDC是平行四边形.
∴DF∥CE.
∵DF?平面PEC,EC?平面PEC.
∴DF∥平面PEC.
(Ⅱ)∵AP⊥平面ABCD,四边形ABCD为矩形,
以点A为坐标原点,建立如图所示的空间直角坐标系A-xyz.
在Rt△PEF中,PE=
| 2 |
可得P(0,0,2),E(1,0,1),C(1,2,0),
∴
| PE |
| PC |
设平面PEC的法向量为
| n |
则
|
|
令x=2,则z=2,y=1,∴
| n |
∵AB⊥平面PAD,∴可取
| AB |
∴cos<
| AB |
| n |
| ||||
|
|
| 2 | ||
|
| 2 |
| 3 |
故平面PEC与平面PAD所成锐二面角的余弦值为
| 2 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 +
+ +
+ = .
= .