题目内容
1.设α、β、γ是三个不同的平面,l、m、n是三条不同的直线,则m⊥β的一个充分条件为②③.①α⊥β,α∩β=l,m⊥l;
②n⊥α,n⊥β,m⊥α;
③α∩γ=m,α⊥β,γ⊥β;
④m⊥α,α⊥γ,β⊥γ.
分析 在①中,m与β相交、平行或m?β;在②中,由线面垂直的性质得m∥n,再由线面垂直判定定理得m⊥β;在③中,由直线与平面垂直判定定理得m⊥β;在④中m与β平行或m?β.
解答 解:由α、β、γ是三个不同的平面,l、m、n是三条不同的直线,知:
①∵α⊥β,α∩β=l,m⊥l,∴m与β相交、平行或m?β,故①错误;
②∵n⊥α,m⊥α,∴m∥n,∵n⊥β,∴m⊥β,故②正确;
③∵α∩γ=m,α⊥β,γ⊥β,∴由直线与平面垂直的判定定理得m⊥β,故③正确;
④∵m⊥α,α⊥γ,β⊥γ,∴m与β平行或m?β,故④错误.
故答案为:②③.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.圆(x-4)2+y2=9和圆x2+(y-3)2=4的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
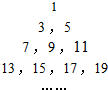 将正奇数排成如图所示的三角形数表:
将正奇数排成如图所示的三角形数表: