题目内容
已知函数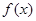 的定义域是
的定义域是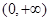 ,
,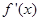 是
是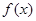 的导函数,且
的导函数,且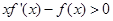 在
在
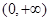 内恒成立.
内恒成立.
求函数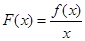 的单调区间;
的单调区间;
若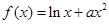 ,求
,求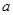 的取值范围;
的取值范围;
(3) 设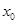 是
是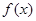 的零点,
的零点, ,求证:
,求证: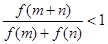 .
.
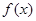 的定义域是
的定义域是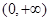 ,
,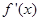 是
是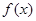 的导函数,且
的导函数,且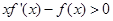 在
在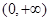 内恒成立.
内恒成立.求函数
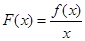 的单调区间;
的单调区间;若
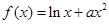 ,求
,求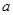 的取值范围;
的取值范围;(3) 设
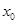 是
是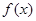 的零点,
的零点, ,求证:
,求证: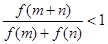 .
.(1)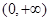 ;(2)
;(2) 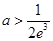 ;(3)详见解析.
;(3)详见解析.
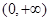 ;(2)
;(2) 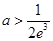 ;(3)详见解析.
;(3)详见解析.试题分析:(1)利用求导的思路求解函数的单调区间,从分借助
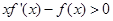 ;(2)首先对
;(2)首先对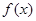 求导,然后借助已知的不等式恒成立进行转化为
求导,然后借助已知的不等式恒成立进行转化为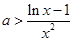 在
在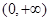 内恒成立,进而采用构造函数的技巧,
内恒成立,进而采用构造函数的技巧,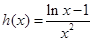 ,通过求导研究其最大值,从而得到
,通过求导研究其最大值,从而得到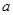 的取值范围;(3)借助第一问结论,得到
的取值范围;(3)借助第一问结论,得到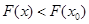 ,然后通过变形和构造的思路去证明不等式成立.
,然后通过变形和构造的思路去证明不等式成立.试题解析:(1)
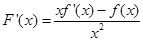 ,∵
,∵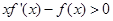 在
在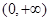 内恒成立
内恒成立∴
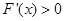 在
在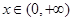 内恒成立,
内恒成立,∴
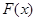 的单调区间为
的单调区间为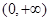 4分
4分(2)
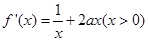 ,∵
,∵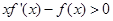 在
在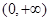 内恒成立
内恒成立∴
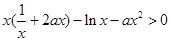 在
在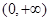 内恒成立,即
内恒成立,即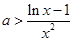 在
在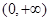 内恒成立,
内恒成立, 设
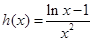 ,
,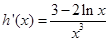
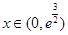 ,
,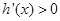 ,
,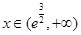 ,
,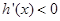 ,
,故函数
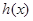 在
在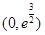 内单调递增,在
内单调递增,在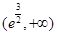 内单调递减,
内单调递减,∴
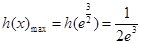 ,∴
,∴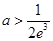 8分
8分(3)∵
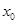 是
是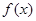 的零点,∴
的零点,∴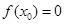 由(1),
由(1),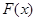 在
在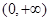 内单调递增,
内单调递增,∴当
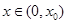 时,
时,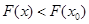 ,即
,即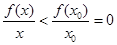 ,
,∴
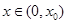 时
时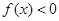 ,∵
,∵ ,∴
,∴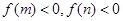 ,
,且
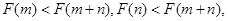 即
即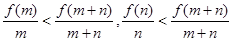
∴
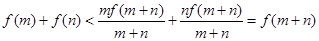 ,
,∴
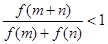 14分
14分
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
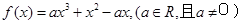
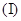 若函数
若函数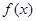 在
在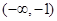 和
和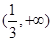 上是增函数,在
上是增函数,在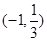 是减函数,求
是减函数,求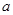 的值;
的值;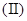 讨论函数
讨论函数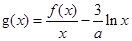 的单调递减区间;
的单调递减区间;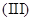 如果存在
如果存在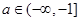 ,使函数
,使函数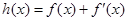 ,
,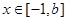
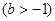 ,在
,在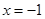 处取得最小值,试求
处取得最小值,试求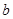 的最大值.
的最大值.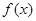 在
在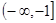 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( ) 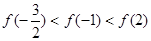
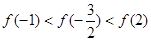
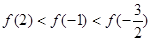
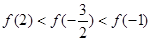
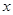 的不等式
的不等式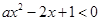 的解集非空的一个必要不充分条件是( )
的解集非空的一个必要不充分条件是( ) 
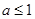
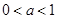
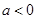
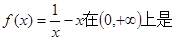 ( )
( ) 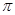 且在
且在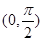 上为增函数的是( )
上为增函数的是( )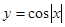
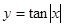
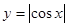
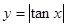
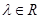 ,
,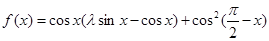 满足
满足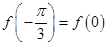 . (1) 求函数
. (1) 求函数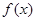 的单调递增区间;
的单调递增区间;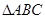 三内角
三内角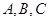 所对边分别为
所对边分别为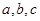 且
且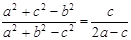 ,求
,求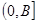 上的值域.
上的值域.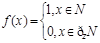 ,则
,则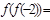 .
.