题目内容
设X~N(10,1).
(1)证明:P(1<X<2)=P(18<X<19);
(2)设P(X≤2)=a,求P(10<X<18).
(1)证明:P(1<X<2)=P(18<X<19);
(2)设P(X≤2)=a,求P(10<X<18).
(1)证明略(2)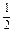 -a
-a
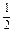 -a
-a(1)证明 因为X~N(10,1),所以,正态曲线P(x)关于直线x=10对称,而区间[1,2]和[18,19]关于直线x=10对称,所以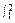 P(x)dx=
P(x)dx=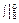 P(x)dx,
P(x)dx,
即P(1<X<2)=P(18<X<19).
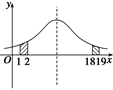
(2)解 P(10<X<18)=P(2<X<10)
=P(X<10)-P(X≤2)=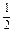 -a.
-a.
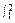 P(x)dx=
P(x)dx=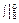 P(x)dx,
P(x)dx,即P(1<X<2)=P(18<X<19).

(2)解 P(10<X<18)=P(2<X<10)
=P(X<10)-P(X≤2)=
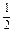 -a.
-a.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
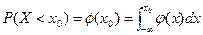 .已知
.已知 ,求下列各式的值:
,求下列各式的值: ; (2)P(|X|<1.44).
; (2)P(|X|<1.44).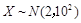 ,若X落在区间
,若X落在区间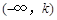 和
和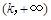 内的概率是相等的,则k等于( )
内的概率是相等的,则k等于( )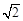
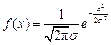 ,
,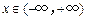 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数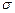 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明. (
( 表示本班学生数学分数),求分数在
表示本班学生数学分数),求分数在 的人数____ ;
的人数____ ;