题目内容
12.若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是3.分析 根据所给x,y的范围,可得|6-x-3y|=6-x-3y,再讨论直线2x+y-2=0将圆x2+y2=1分成两部分,分别去绝对值,运用线性规划的知识,平移即可得到最小值.
解答 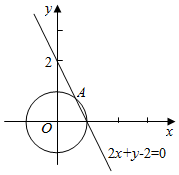 解:由x2+y2≤1,可得6-x-3y>0,即|6-x-3y|=6-x-3y,
解:由x2+y2≤1,可得6-x-3y>0,即|6-x-3y|=6-x-3y,
如图直线2x+y-2=0将圆x2+y2=1分成两部分,
在直线的上方(含直线),即有2x+y-2≥0,即|2x+y-2|=2x+y-2,
此时|2x+y-2|+|6-x-3y|=(2x+y-2)+(6-x-3y)=x-2y+4,
利用线性规划可得在A($\frac{3}{5}$,$\frac{4}{5}$)处取得最小值3;
在直线的下方(含直线),即有2x+y-2≤0,
即|2x+y-2|=-(2x+y-2),
此时|2x+y-2|+|6-x-3y|=-(2x+y-2)+(6-x-3y)=8-3x-4y,
利用线性规划可得在A($\frac{3}{5}$,$\frac{4}{5}$)处取得最小值3.
综上可得,当x=$\frac{3}{5}$,y=$\frac{4}{5}$时,|2x+y-2|+|6-x-3y|的最小值为3.
故答案为:3.
点评 本题考查直线和圆的位置关系,主要考查二元函数在可行域内取得最值的方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
7.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
17.“x>1”是“$lo{g_{\frac{1}{2}}}$(x+2)<0”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
1.执行如图所示的程序框图,则输出s的值为( )


| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
2.阅读如图所示的程序框图,运行相应的程序,若输入x的值为1,则输出y的值为( )
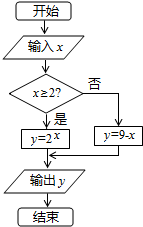

| A. | 2 | B. | 7 | C. | 8 | D. | 128 |
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1(-1,0),F2(1,0),过右焦点F2,且斜率为k(k≠0)的直线l与椭圆C相交于M,N两点,△MNF1的周长是8.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1(-1,0),F2(1,0),过右焦点F2,且斜率为k(k≠0)的直线l与椭圆C相交于M,N两点,△MNF1的周长是8.