题目内容
2. 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1(-1,0),F2(1,0),过右焦点F2,且斜率为k(k≠0)的直线l与椭圆C相交于M,N两点,△MNF1的周长是8.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1(-1,0),F2(1,0),过右焦点F2,且斜率为k(k≠0)的直线l与椭圆C相交于M,N两点,△MNF1的周长是8.(1)求椭圆C的方程;
(2)椭圆右顶点为A,直线MA,NA分别交直线l':x=5于点P,Q,线段PQ的中点为R,记直线F1R的斜率为k',求证kk'为定值,并求这个定值.
分析 对于第(1)问,先由焦点坐标,得c的值,再由周长得a2的值,根据b2=a2-c2,得b2,即得椭圆的标准方程;
对于第(2)问,先设出交点P,Q及中点为R的坐标,于是写出直线MA,NA的方程,联立x=5,即可表示P,Q的坐标,从而得R的坐标,接着由两点的斜率公式,写出斜率k'的表达式,再联立直线l与椭圆的方程,得到一个关于x的一元二次方程,由韦达定理,得x1+x2,x1x2,可进一步用k表示k',最后可计算kk'的值.
解答 解:(1)设焦距为2c,则依题意有c=1.
由△MNF1的周长是8,(|MF1|+|MF2|)+(|NF1|+|NF2|)=4a=8,
即得a2=4,从而b2=a2-c2=3,
所以椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)设点M,N的坐标分别为(x1,y1),(x2,y2),点A的坐标为(2,0),
则直线MA,NA的方程分别为:(x1-2)y=y1(x-2),(x2-2)y=y2(x-2),
联立x=5,得交点P$(5,\frac{3{y}_{1}}{{x}_{1}-2})$,Q$(5,\frac{3{y}_{2}}{{x}_{2}-2})$,
由中点公式,得点R的坐标为$(5,\frac{1}{2}(\frac{{3{y_1}}}{{{x_1}-2}}+\frac{{3{y_2}}}{{{x_2}-2}}))$,
所以$k'=\frac{{\frac{1}{2}(\frac{{3{y_1}}}{{{x_1}-2}}+\frac{{3{y_2}}}{{{x_2}-2}})}}{5-(-1)}=\frac{1}{4}(\frac{y_1}{{{x_1}-2}}+\frac{y_2}{{{x_2}-2}})$.
又设直线l的方程为y=k(x-1),代入椭圆方程中,
得3x2+4k2(x-1)2=12,即(3+4k2)x2-8k2x+4k2-12=0,
由韦达定理,得${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}},{x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$,
所以$kk'=\frac{k^2}{4}•\frac{{({x_1}-1)({x_2}-2)+({x_2}-1)({x_1}-2)}}{{({x_1}-2)({x_2}-2)}}$
=$\frac{k^2}{4}•\frac{{2{x_1}{x_2}-3({x_1}+{x_2})+4}}{{{x_1}{x_2}-2({x_1}+{x_2})+4}}$=$\frac{k^2}{4}•\frac{{8{k^2}-24-24{k^2}+16{k^2}+12}}{{4{k^2}-12-16{k^2}+16{k^2}+12}}=-\frac{3}{4}$,
即kk'为定值$-\frac{3}{4}$.
点评 本题属定值的证明问题,主要考查了椭圆标准方程的求法,直线与椭圆相交的位置关系等,求解时,应注意以下几点:
①椭圆方程的确定,除了隐含条件a2=b2+c2以外,还要寻找关于a,b,c的两个独立的方程;
②对于定值的证明问题,关键是先引入参数(如点的坐标,直线的斜率,纵截距等),再用参数表示所证式,最后通过消参的方式获取定值,其间,韦达定理往往起到重要的作用.

| A. | p是q的充分条件,但不是q的必要条件 | |
| B. | p是q的必要条件,但不是q的充分条件 | |
| C. | p是q的充分必要条件 | |
| D. | p既不是q的充分条件,也不是q的必要条件 |
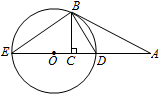 如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.
如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.