题目内容
【题目】如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB= 
，AF=1，M是线段EF的中点． 
（Ⅰ）求证AM∥平面BDE；
（Ⅱ）求二面角A﹣DF﹣B的大小．
【答案】解：方法一（Ⅰ）记AC与BD的交点为O，连接OE，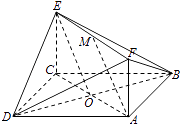
∵O、M分别是AC、EF的中点，ACEF是矩形，
∴四边形AOEM是平行四边形，
∴AM∥OE
∵OE平面BDE，AM平面BDE，
∴AM∥平面BDE
（Ⅱ）在平面AFD中过A作AS⊥DF于S，连接BS，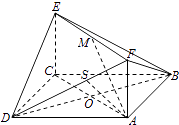
∵AB⊥AF，AB⊥AD，AD∩AF=A，
∴AB⊥平面ADF，
∴AS是BS在平面ADF上的射影，
由三垂线定理得BS⊥DF
∴∠BSA是二面角A﹣DF﹣B的平面角
在Rt△ASB中，AS= 
= 
，AB= 
，
∴ 
，
∴二面角A﹣DF﹣B的大小为60°
方法二
（Ⅰ）建立如图所示的空间直角坐标系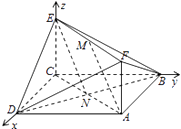
设AC∩BD=N，连接NE，
则点N、E的坐标分别是（ 
、（0，0，1），
∴ 
=（ 
，
又点A、M的坐标分别是
（ 
）、（ 
∴ 
=（
∴ 
= 且NE与AM不共线，
∴NE∥AM
又∵NE平面BDE，AM平面BDE，
∴AM∥平面BDF
（Ⅱ）∵AF⊥AB，AB⊥AD，AF∩AD=A，
∴AB⊥平面ADF
∴ 
为平面DAF的法向量
∵ 
=（ 
=0，
∴ 
=（ 
=0得 
， 
∴NE为平面BDF的法向量
∴cos＜ 
＞= 
∴ 的夹角是60°
即所求二面角A﹣DF﹣B的大小是60°
【解析】（Ⅰ）要证AM∥平面BDE，直线证明直线AM平行平面BDE内的直线OE即可，也可以利用空间直角坐标系，求出向量 
，在平面BDE内求出向量 
，证明二者共线，说明AM∥平面BDE，（Ⅱ）在平面AFD中过A作AS⊥DF于S，连接BS，说明∠BSA是二面角A﹣DF﹣B的平面角，然后求二面角A﹣DF﹣B的大小；也可以建立空间直角坐标系，求出 
， 
说明 是平面DFB的法向量，求出平面DAF的法向量 
，然后利用数量积求解即可．
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能正确解答此题．
