题目内容
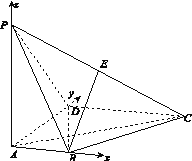
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
【答案】(1)见解析(2) ![]() (3)
(3) ![]()
【解析】试题分析:(I)以A为坐标原点,建立如图所示的空间直角坐标系,求出BE,DC的方向向量,根据
![]() ,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量
,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量![]() 的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F-AB-P的余弦值
的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F-AB-P的余弦值
试题解析:方法一:依题意,以点A为原点建立空间直角坐标系(如图所示),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).C由E为棱PC的中点,得E(1,1,1).
(1)证明:向量![]() =(0,1,1),
=(0,1,1),![]() =(2,0,0),
=(2,0,0),
故![]() =0,
=0,
所以BE⊥DC.
(2)向量![]() =(-1,2,0),
=(-1,2,0),![]() =(1,0,-2).
=(1,0,-2).
设n=(x,y,z)为平面PBD的法向量,
则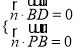
![]()
不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量.于是有
![]() =
=![]() =
=![]() =
=![]() ,
,
所以直线BE与平面PBD所成角的正弦值为![]() .
.
(3) 向量![]() =(1,2,0),
=(1,2,0),![]() =(-2,-2,2),
=(-2,-2,2),![]() =(2,2,0),
=(2,2,0),![]() =(1,0,0).
=(1,0,0).
由点F在棱PC上,设![]() =λ
=λ![]() ,0≤λ≤1.
,0≤λ≤1.
故![]() =
=![]() +
+![]() =
=![]() +λ
+λ![]() =(1-2λ,2-2λ,2λ).由BF⊥AC,得
=(1-2λ,2-2λ,2λ).由BF⊥AC,得![]() =0,因此2(1-2λ)+2(2-2λ)=0,解得λ=
=0,因此2(1-2λ)+2(2-2λ)=0,解得λ=![]() ,即
,即![]() =
=![]() .设n1=(x,y,z)为平面FAB的法向量,
.设n1=(x,y,z)为平面FAB的法向量,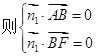 即
即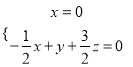 不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.取平面ABP的法向量n2=(0,1,0),则
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.取平面ABP的法向量n2=(0,1,0),则
cos〈n1,n2〉=![]() =
=![]() =-
=-![]() .
.
易知二面角F AB P是锐角,所以其余弦值为![]() .
.
方法二:(1)证明:如图所示,取PD中点M,连接EM,AM.由于E,M分别为PC,PD的中点,故EM∥DC,且EM=![]() DC.又由已知,可得EM∥AB且EM=AB,故四边形ABEM为平行四边形,所以BE∥AM.
DC.又由已知,可得EM∥AB且EM=AB,故四边形ABEM为平行四边形,所以BE∥AM.
因为PA⊥底面ABCD,故PA⊥CD,而CD⊥DA,从而CD⊥平面PAD.因为AM平面PAD,所以CD⊥AM.又BE∥AM,所以BE⊥CD.
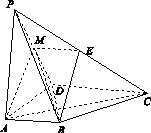
(2)连接BM,由(1)有CD⊥平面PAD,得CD⊥PD.而EM∥CD,故PD⊥EM.又因为AD=AP,M为PD的中点,所以PD⊥AM,可得PD⊥BE,所以PD⊥平面BEM,故平面BEM⊥平面PBD,所以直线BE在平面PBD内的射影为直线BM.而BE⊥EM,可得∠EBM为锐角,故∠EBM为直线BE与平面PBD所成的角.
依题意,有PD=2![]() ,而M为PD中点,可得AM=
,而M为PD中点,可得AM=![]() ,进而BE=
,进而BE=![]() .故在直角三角形BEM中,tan∠EBM=
.故在直角三角形BEM中,tan∠EBM=![]() =
=![]() =
=![]() ,因此sin∠EBM=
,因此sin∠EBM=![]() ,
,
所以直线BE与平面PBD所成角的正弦值为![]() .
.
(3)如图所示,在△PAC中,过点F作FH∥PA交AC于点H.因为PA⊥底面ABCD,所以FH⊥底面ABCD,从而FH⊥AC.又BF⊥AC,得AC⊥平面FHB,因此AC⊥BH.在底面ABCD内,可得CH=3HA,从而CF=3FP.在平面PDC内,作FG∥DC交PD于点G,于是DG=3GP.由于DC∥AB,故GF∥AB,所以A,B,F,G四点共面.由AB⊥PA,AB⊥AD,得AB⊥平面PAD,故AB⊥AG,所以∠PAG为二面角F AB P的平面角.
在△PAG中,PA=2,PG=![]() PD=
PD=![]() ,∠APG=45°.由余弦定理可得AG=
,∠APG=45°.由余弦定理可得AG=![]() ,cos∠PAG=
,cos∠PAG=![]() ,所以二面角F AB P的余弦值为
,所以二面角F AB P的余弦值为![]() .
.

