题目内容
【题目】已知函数f(x)=(![]() )x.
)x.
(Ⅰ)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值g(a);
(Ⅱ)在(Ⅰ)的条件下,是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由.
【答案】(Ⅰ)g(a)=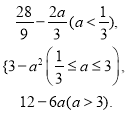 (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)在![]() 的情况下,求出
的情况下,求出![]() 的值域,对所给函数进行配方化简,可利用一元二次函数的性质对
的值域,对所给函数进行配方化简,可利用一元二次函数的性质对![]() 进行分类讨论,可得函数的最小值
进行分类讨论,可得函数的最小值![]() ;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在
;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在![]() 的单调性,结合区间与值域,可得关于
的单调性,结合区间与值域,可得关于![]() 的等式,解得
的等式,解得![]() 存在情况.
存在情况.
试题解析:(Ⅰ)∵x∈[﹣1,1],∴f(x)=(![]() )x∈[
)x∈[![]() ,3],
,3],
y=[f(x)]2﹣2af(x)+3=[(![]() )x]2﹣2a(
)x]2﹣2a(![]() )x+3
)x+3
=[(![]() )x﹣a]2+3﹣a2. .
)x﹣a]2+3﹣a2. .
由一元二次函数的性质分三种情况:
若a<![]() ,则当
,则当![]() 时,ymin=g(a)=
时,ymin=g(a)=![]() ;
;
若![]() ≤a≤3,则当
≤a≤3,则当![]() 时,ymin=g(a)=3﹣a2;
时,ymin=g(a)=3﹣a2;
若a>3,则当![]() 时,ymin=g(a)=12﹣6a.
时,ymin=g(a)=12﹣6a.
∴g(a)=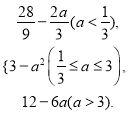
(Ⅱ)假设存在满足题意的m、n,
∵m>n>3,且g(x)=12﹣6x在区间(3,+∞)内是减函数,
又g(x)的定义域为[n,m],值域为[n2,m2],
∴![]()
两式相减,得6(m﹣n)=(m+n)(m﹣n),
∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,
∴满足题意的m、n不存在.

练习册系列答案
相关题目