Question

【题目】如图所示，已知点是抛物线上一定点，直线的斜率互为相反数，且与抛物线另交于两个不同的点．

（1）求点到其准线的距离；（2）求证：直线的斜率为定值．

Answer 1

【答案】（1）；（2）证明见解析．

【解析】试题分析：（1）根据点在抛物线上得到参数值，再根据抛物线的定义得到点到准线的距离；（2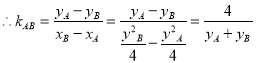），联立直线和抛物线得到二次方程，根据韦达定理得到斜率为定值。

解析：

（1）解：∵M（a，3）是抛物线y2=4x上一定点

∴32=4a，

∵抛物线y2=4x的准线方程为x=﹣1

∴点M到其准线的距离为： ．

（2）证明：由题知直线MA、MB的斜率存在且不为0，

设直线MA的方程为：

联立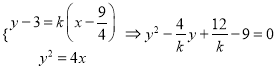

∵直线AM、BM的斜率互为相反数

∴直线MA的方程为：y﹣3=﹣k（x﹣），

同理可得：

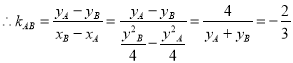
∴直线AB的斜率为定值﹣．