题目内容
3.某城市小汽车的普及率为40%,即平均10个家庭有小汽车,若从这个城市中任意选出5个家庭,则2个以上(含2个)的家庭有小汽车的概率为0.66304.分析 设抽取的家庭中有小汽车的事件为A,则p=P(A)=0.4,q=P($\overline{A}$)=0.6,则所求概率满足二项分布,继而所求.
解答 解:设抽取的家庭中有小汽车的事件为A,
则p=P(A)=0.4,q=P($\overline{A}$)=0.6,则所求概率满足二项分布,
故P(k≥2)=1-P(k<2)=1-P(0)-P(1)=1-${C}_{5}^{0}$×0.65-${C}_{5}^{1}$×0.4×0.64=0.66304,
故答案为:0.66304.
点评 本题考查了服从二项分布的概率问题,属于基础题.

练习册系列答案
相关题目
13.若m=1!+2!+3!+4!+5!+…+2014!+2015!,则m的个位数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.满足条件|z-i|+|z+i|=3的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
 函数f(x)=ax+b的图象如图,其中a,b为常数,给出下列四种说法:①a>1,b>0;②0<a<1,b<0;③a>1,b>-1;④a>1,b<-1.则其中所有正确说法的序号是④.
函数f(x)=ax+b的图象如图,其中a,b为常数,给出下列四种说法:①a>1,b>0;②0<a<1,b<0;③a>1,b>-1;④a>1,b<-1.则其中所有正确说法的序号是④.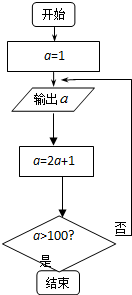 按照如图所示的框图操作,
按照如图所示的框图操作,