题目内容
4.已知集合A={x|x<-1或x≥1},B={x|x≤2a或x≥a+1},若(∁RB)⊆A,求实数a的取值范围.分析 化简集合∁RB={x|2a<x<a+1},从而分类讨论以确定集合是否是空集,从而解得.
解答 解:∵B={x|x≤2a或x≥a+1},
∴∁RB={x|2a<x<a+1},
当2a≥a+1,即a≥1时,∁RB=∅⊆A,
当2a<a+1,即a<1时,∁RB≠∅,
要使∁RB⊆A,
应满足a+1≤-1或是2a≥1,
即a≤-2或$\frac{1}{2}≤a<1$,
综上可知,实数a的取值范围为a≤-2或a≥$\frac{1}{2}$.
点评 本题考查了集合的化简与集合的运算.

练习册系列答案
相关题目
16.函数f(x)=lo${g}_{\frac{1}{2}}$(x2-ax)在区间[2,4]上是减函数,则实数a的取值范围是( )
| A. | 2<a≤4 | B. | a≤4 | C. | a<2 | D. | a≤2 |
14.抛物线y=$\frac{1}{4}$x2的焦点关于直线x-y-1=0的对称点的坐标是 ( )
| A. | (2,-1) | B. | (1,-1) | C. | ($\frac{1}{4}$,-$\frac{1}{4}$) | D. | ($\frac{1}{16}$,-$\frac{1}{16}$) |
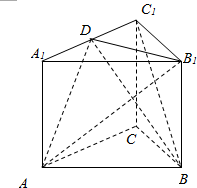 如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧楞长为$\sqrt{2}$,D为A1C1中点.
如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧楞长为$\sqrt{2}$,D为A1C1中点.