题目内容
【题目】在数列{an}中,a1=1,an+1=2an+2n .
(1)设bn= ![]() ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.
(2)求数列{an}的前n项和.
【答案】
(1)证明:∵an+1=2an+2n,∴ ![]() ,
,
∴bn+1﹣bn=1.
∴数列{bn}是等差数列,首项为 ![]() =1,公差为1
=1,公差为1
(2)解:由(1)可得:bn=1+(n﹣1)=n,
∴ ![]() ,
,
∴ ![]() ,
,
∴数列{an}的前n项和Sn=1+2×2+3×22+…+n2n﹣1,
2Sn=2+2×22+3×23+…+(n﹣1)×2n﹣1+n×2n,
∴﹣Sn=1+2+22+…+2n﹣1﹣n×2n= ![]() ﹣n×2n=(1﹣n)×2n﹣1.
﹣n×2n=(1﹣n)×2n﹣1.
∴Sn=(n﹣1)×2n+1
【解析】(1)由an+1=2an+2n , 可得 ![]() ,即bn+1﹣bn=1.即可证明;(2)由(1)可得:bn=1+(n﹣1)=n,
,即bn+1﹣bn=1.即可证明;(2)由(1)可得:bn=1+(n﹣1)=n, ![]() ,再利用“错位相减法”、等比数列的前n项和公式即可得出.
,再利用“错位相减法”、等比数列的前n项和公式即可得出.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系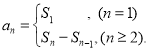 .
.

练习册系列答案
相关题目