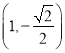题目内容
【题目】已知数列{an}是一个公差大于0的等差数列,且满足![]() ,a2+a7=16
,a2+a7=16
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式![]() (n∈N*),求数列{bn}的前n项和Sn.
(n∈N*),求数列{bn}的前n项和Sn.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
![]() 设等差数列
设等差数列![]() 的公差为
的公差为![]() ,分别表示出
,分别表示出![]() 联立方程求得
联立方程求得![]() 和
和![]() ,进而根据等差数列通项公式求得
,进而根据等差数列通项公式求得![]()
![]() 令
令![]() ,则有
,则有![]() ,两式相减求得
,两式相减求得![]() 等于常数
等于常数![]() ,进而可得
,进而可得![]() ,进而根据
,进而根据![]() ,求得
,求得![]() ,则数列
,则数列![]() 通项公式可得,进而根据从第二项开始按等比数列求和公式求和再加上
通项公式可得,进而根据从第二项开始按等比数列求和公式求和再加上![]()
解:(1)设等差数列{an}的公差为d,
则依题意可知d>0由a2+a7=16,
得2a1+7d=16①
由![]() =55,得(a1+2d)(a1+5d)=55②
=55,得(a1+2d)(a1+5d)=55②
由①②联立方程求得
得d=2,a1=1或d=﹣2,a1=![]() (排除)
(排除)
∴an=1+(n﹣1)2=2n﹣1
令cn=![]() ,则有an=c1+c2+…+cn
,则有an=c1+c2+…+cn
an+1=c1+c2+…+cn+1
两式相减得
an+1﹣an=cn+1,由(1)得a1=1,an+1﹣an=2
∴cn+1=2,即cn=2(n≥2),
即当n≥2时,
bn=2n+1,又当n=1时,b1=2a1=2
∴bn=![]()
于是Sn=b1+b2+b3+…+bn=2+23+24+…2n+1=2n+2﹣6, ![]()
![]()

练习册系列答案
相关题目