题目内容
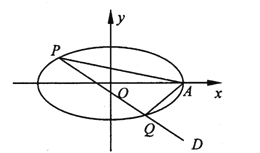
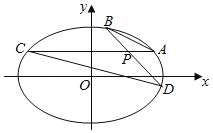
【题目】已知椭圆
，倾斜角为
的直线与椭圆相交于
两点，且线段
的中点为
．过椭圆
内一点
的两条直线分别与椭圆交于点
，且满足
，其中
为实数．当直线
平行于
轴时，对应的
．
（Ⅰ）求椭圆的方程；
（Ⅱ）当变化时，
是否为定值？若是，请求出此定值；若不是，请说明理由．
【答案】（Ⅰ）
； （Ⅱ）
.
【解析】
（Ⅰ）将M和N点坐标代入椭圆方程，根据斜率公式求得kMN=1，求得a和b的关系，当直线AP平行于x轴时，设|AC|=2d，求得A点坐标，代入椭圆方程，即可求得a和b，求得椭圆方程；
（Ⅱ）设出A、B、C和D点坐标，由向量共线，
=λ
，
=λ
，及A和B在椭圆上，利用斜率公式，kAB=kCD，求得3（1+λ）kAB=﹣2（1+λ），即可求得kAB为定值．
（Ⅰ）设M（m1，n1）、N（m2，n2），则
，
两式相减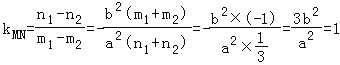
，
故a2=3b2
当直线AP平行于x轴时，设|AC|=2d，
∵
，
，则
，解得
，
故点A（或C）的坐标为
．
代入椭圆方程
，得
a2=3，b2=1，
所以方程为
.
（Ⅱ）设A（x1，y1）、B（x2，y2）、C（x3，y3）、D（x4，y4）
由于
，可得A（x1，y1）、B（x2，y2）、C（x3，y3）、D（x4，y4），
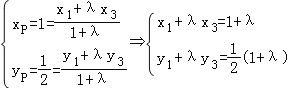…①
同理
可得
…②
由①②得：
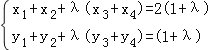…③
将点A、B的坐标代入椭圆方程得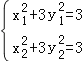
，
两式相减得（x1+x2）（x1﹣x2）+3（y1+y2）（y1﹣y2）=0，
于是3（y1+y2）kAB=﹣（x1+x2）…④
同理可得：3（y3+y4）kCD=﹣（x3+x4），
于是3（y3+y4）kAB=﹣（x3+x4）（∵AB∥CD，∴kAB=kCD）
所以3λ（y3+y4）kAB=﹣λ（x3+x4）…⑤
由④⑤两式相加得到：3[y1+y2+λ（y3+y4）]kAB=﹣[（x1+x2）+λ（x3+x4）]
把③代入上式得3（1+λ）kAB=﹣2（1+λ），
解得：
，
当λ变化时，kAB为定值，．
