Question

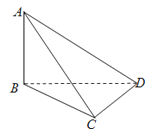
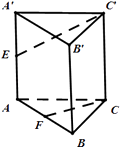
【题目】如图，在三棱柱ABC﹣A1B1C1中，已知AB⊥侧面BB1C1C，CB⊥C1B，BC=1，CC1=2，A1B1= ，
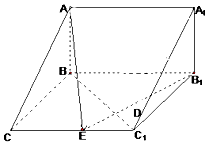
（1）试在棱CC1（不包含端点C，C1）上确定一点E的位置，使得EA⊥EB1；
（2）在（1）的条件下，求AE和BC1所成角．

Answer 1

【答案】
（1）解：由EA⊥EB1，AB⊥EB1，AB∩AE=A，AB，AE平面ABE，

从而B1E⊥平面ABE且BE平面ABE，故BE⊥B1E．

不妨设 CE=x，则C1E=2﹣x，

∵∠BCC1=60°，∴BE2=1+x2﹣x，

∵∠BCC1=60°，∴∠B1C1C=120°，∴ ．

在Rt△BEB1中有1+x2﹣x+x2﹣5x+7=4，

从而x=1或x=2（当x=2时E与C1重合不满足题意）．

故E为CC1的中点时，EA⊥EB1

（2）解：取BC中点D，则DE∥BC1，连接AD，

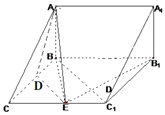
所以∠AED或其补角为异面直线AE和BC1所成角所成的角．

∵ ，

∴cos∠AED= = ，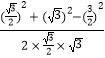

∴∠AED=60°．

【解析】（1）由EA⊥EB1 ， AB⊥EB1 ， AB∩AE=A，AB，AE平面ABE，从而B1E⊥平面ABE且BE平面ABE，故BE⊥B1E．利用余弦定理及其勾股定理即可得出．（2）取BC中点D，则DE∥BC1 ， 连接AD，所以∠AED或其补角为异面直线AE和BC1所成角所成的角． 利用余弦定理即可得出．
【考点精析】本题主要考查了棱柱的结构特征和异面直线及其所成的角的相关知识点，需要掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形；异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．