题目内容
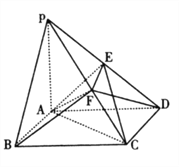
【题目】已知△ABC中,顶点A(3,7),边AB上的中线CD所在直线的方程是![]() ,边AC上的高BE所在直线的方程是
,边AC上的高BE所在直线的方程是![]() .
.
(1)求点A关于直线CD的对称点的坐标;
(2)求顶点B、C的坐标;
(3)过A作直线![]() ,使B,C两点到
,使B,C两点到![]() 的距离相等,求直线
的距离相等,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)设点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的中点需在直线
的中点需在直线![]() :
:![]() 上,且
上,且![]() ,得到方程组,解得即可;
,得到方程组,解得即可;
(2)依题意设![]() 所在直线方程为
所在直线方程为![]() ,联立
,联立![]() 与
与![]() ,求得其交点即为
,求得其交点即为![]() ,
,
设![]() 则
则![]() 的中点坐标为
的中点坐标为![]() ,则
,则![]() 的中点在直线
的中点在直线![]() 上,且
上,且![]() 在
在![]() 上,联立解得;
上,联立解得;
(3)分两种情况讨论: 当直线![]() 过
过![]() 的中点,显然满足
的中点,显然满足![]() 、
、![]() 两点到
两点到![]() 的距离相等;
的距离相等;
当直线![]() 平行
平行![]() 时,也满足
时,也满足![]() 、
、![]() 两点到
两点到![]() 的距离相等;分别计算可得;
的距离相等;分别计算可得;
解:(1)设点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() 的中点坐标为
的中点坐标为![]() ,
,
因为![]() :
:![]() ,
,![]()
所以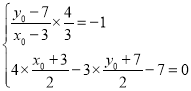 解得
解得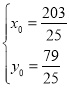 故对称点的坐标为
故对称点的坐标为![]() ;
;
(2)依题意设![]() 所在直线方程为
所在直线方程为![]() ,
,
则![]() 解得
解得![]() ,故
,故![]()
所以![]() 解得
解得![]() 故
故![]() ,
,
设![]() 则
则![]() 的中点坐标为
的中点坐标为![]() ,
,
所以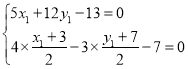 ,解得
,解得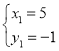
即![]()
(3)由(2)可得![]() 的中点坐标为
的中点坐标为![]() ,当直线
,当直线![]() 过
过![]() 的中点,显然满足
的中点,显然满足![]() 、
、![]() 两点到
两点到![]() 的距离相等,此时直线方程为
的距离相等,此时直线方程为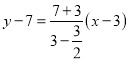 ,即
,即![]() ;
;
当直线![]() 平行
平行![]() 时,也满足
时,也满足![]() 、
、![]() 两点到
两点到![]() 的距离相等,此时直线方程为
的距离相等,此时直线方程为![]() ,即
,即![]()
故满足条件的直线方程为![]() 或
或![]()

练习册系列答案
相关题目