Question

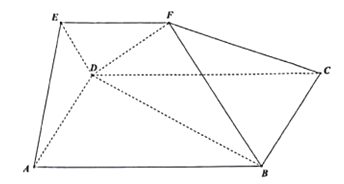
【题目】已知四棱锥，底面为正方形，且底面，过的平面与侧面的交线为，且满足（表示的面积）.

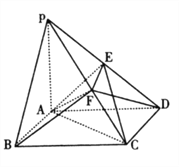
（1）证明： 平面；

（2）当时，求点到平面的距离.

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：（1）利用平几知识由S△PEF：S四边形CDEF=1:3知E为PC的中点，连接BD交AC与G，则G为BD中点，由三角形中位线性质得EG//PB，再根据线面平行判定定理得结果（2）先根据中点得,再根据等体积法得,根据CD⊥平面PAD，得高CD，利用锥体体积公式得，即得，最后根据高等于点到平面的距离

试题解析：（Ⅰ）证明：由题知四边形ABCD为正方形

∴AB//CD，又平面PCD，AB平面PCD

∴AB//平面PCD

又AB平面ABFE，平面ABFE∩平面PCD=EF

∴EF // AB，又AB//CD

∴EF //CD，

由S△PEF：S四边形CDEF=1:3知E、F分别为PC、PD的中点

连接BD交AC与G，则G为BD中点，

在△PBD中FG为中位线，∴ EG//PB

∵ EG//PB，EG平面ACE，PB平面ACE

∴PB//平面ACE.

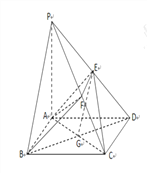
（Ⅱ）∵PA=2，AD=AB=1， ∴,

∵CD⊥AD，CD⊥PA，AD∩PA=A，

∴CD⊥平面PAD，∴CD⊥PD

在Rt△CDE中，

在△ACE中由余弦定理知

∴，∴S△ACE=

设点F到平面ACE的距离为，则

由DG⊥AC，DG⊥PA，AC∩PA=A，得DG⊥平面PAC，且

∵E为PD中点，∴E到平面ACF的距离为

又F为PC中点，∴S△ACF S△ACP ，∴

由知

∴点F到平面ACE的距离为.