题目内容
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且C与y轴交于
,且C与y轴交于![]() 两点.
两点.
(1)求椭圆C的标准方程;
(2)设P点是椭圆C上的一个动点且在y轴的右侧,直线PA,PB与直线![]() 交于M,N两点.若以MN为直径的圆与x轴交于E,F两点,求P点横坐标的取值范围.
交于M,N两点.若以MN为直径的圆与x轴交于E,F两点,求P点横坐标的取值范围.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)由椭圆![]() 的焦距为
的焦距为![]() ,可得
,可得![]() ,由
,由![]() 可得
可得![]() ,结合
,结合![]() 可得
可得![]() ,进而可得结果;(2)设
,进而可得结果;(2)设![]() ,可得
,可得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,同理得直线
,同理得直线![]() 的方程为
的方程为![]() , 求得
, 求得![]() ,
,![]() ,可得圆的方程为
,可得圆的方程为![]() ,利用这个圆与
,利用这个圆与![]() 轴相交,方程有两个不同的实数解,即可得结果.
轴相交,方程有两个不同的实数解,即可得结果.
试题解析:(Ⅰ)由题意可得,![]() ,
,![]() 所以
所以![]() ,, 椭圆
,, 椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
同理得直线![]() 的方程为
的方程为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中点
的中点![]() ,
,
所以圆的方程为![]() .
.
令![]() ,则
,则![]() , 因为
, 因为![]() ,所以
,所以![]() ,
,
因为这个圆与![]() 轴相交,所以该方程有两个不同的实数解,
轴相交,所以该方程有两个不同的实数解,
则![]() ,又0
,又0![]() ,解得
,解得![]() .
.
解法二:直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 联立得:
联立得:![]() ,
,![]() ,
,
同理设![]() 直线的方程为
直线的方程为![]() 可得
可得![]() ,
,
由![]()
![]() ,可得
,可得![]() ,
,
所以![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,
所以![]() 为直径的圆为
为直径的圆为![]() .
.
![]() 时,
时,![]() ,所以
,所以![]() ,
,
因为![]() 为直径的圆与
为直径的圆与![]() 轴交于
轴交于![]() 两点,所以
两点,所以![]() ,
,
代入![]() 得:
得:![]() ,所以
,所以![]() ,
,
所以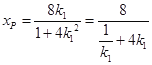 在
在![]() 单增,在
单增,在![]() 单减,所以
单减,所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目