Question

【题目】已知函数f（x）=x﹣1+ ，（a∈R，e为自然对数的底数）．
（1）求函数f（x）的单调区间；
（2）当a=1时，若直线l：y=kx﹣1与曲线y=f（x）没有公共点，求k的最大值．

Answer 1

【答案】
（1）解：∵f（x）=x﹣1+ ，

∴f′（x）=1﹣ = ，由f′（x）=0得x=lna

∴当x∈（﹣∞，lna）时，f′（x）＜0，∴（﹣∞，lna）是f（x）的单调递减区间；

当x∈（lna，+∞）时，f′（x）＞0，∴（lna，+∞）是f（x）的单调递增区间

（2）解：当a=1时，若直线l：y=kx﹣1与曲线y=f（x）=x﹣1+ 没有公共点，则x﹣1+ =kx﹣1无解，

∵x=0时，上述方程不成立，∴x≠0

则x﹣1+ =kx﹣1可化为k=1+ ，

设g（x）=1+ ，∴g′（x）=

∴g′（x）满足：在（﹣∞，﹣1）上g′（x）＞0，在（﹣1，0）上g′（x）＜0，在（0，+∞）上g′（x）＜0，

∴g（x）满足：在（﹣∞，﹣1）上递增，在（﹣1，0）上递减，在（0，+∞）上递减，

g（﹣1）=1﹣e，而当x→+∞时，g（x）→1，

∴g（x）的图象：

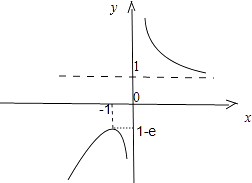
∴g（x）∈（﹣∞，1﹣e]∪（1，+∞）

无解时，k∈（1﹣e，1]，

∴kmax=1

【解析】（1）先求导，f′（x）=1﹣ = ，由f′（x）=0得x=lna，分x∈（﹣∞，lna）与（﹣∞，lna）两种情况写出f（x）的单调递减区间；（2）当a=1时，若直线l：y=kx﹣1与曲线y=f（x）=x﹣1+ 没有公共点，则x﹣1+ =kx﹣1无解，则x﹣1+ =kx﹣1可化为k=1+ ，
设g（x）=1+ ，求导，研究此函数的单调性即可解决．
【考点精析】根据题目的已知条件，利用函数的最值及其几何意义和利用导数研究函数的单调性的相关知识可以得到问题的答案，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．