题目内容
12.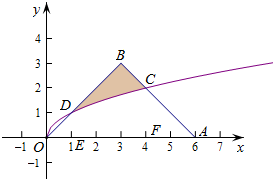 如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{27}$ | D. | $\frac{11}{54}$ |
分析 求出C的坐标,根据几何概型的概率公式求出对应的面积进行求解即可.
解答 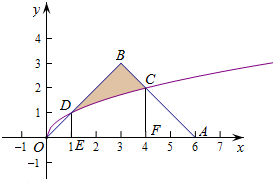 解:∵顶点A,B的坐标分别为(6,0),(3,3),
解:∵顶点A,B的坐标分别为(6,0),(3,3),
∴AB的方程为$\frac{y-0}{3-0}=\frac{x-6}{3-6}$,
即y=-x+6,
由$\left\{\begin{array}{l}{y=-x+6}\\{y=\sqrt{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,即C(4,2),
0B的方程为y=x,
由$\left\{\begin{array}{l}{y=x}\\{y=\sqrt{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即D(1,1),
则△ODE的面积S=$\frac{1}{2}×1×1=\frac{1}{2}$,
则△AFC的面积S=$\frac{1}{2}×2×2=2$,
△OAB的面积S=$\frac{1}{2}×6×3=9$,
曲边四边形DEFC的面积S=${∫}_{1}^{4}\sqrt{x}$dx=$\frac{2}{3}$x${\;}^{\frac{3}{2}}$|${\;}_{1}^{4}$=$\frac{16}{3}-\frac{2}{3}=\frac{14}{3}$,
则阴影部分的面积S=9-$\frac{1}{2}-\frac{14}{3}$-2=$\frac{23}{6}$-2=$\frac{11}{6}$,
故点P落在阴影部分的概率为$\frac{\frac{11}{6}}{9}$=$\frac{11}{54}$,
故选:D.
点评 本题主要考查几何概型的概率的计算,根据条件求出C的坐标以及阴影部分的面积是解决本题的关键.

 初中暑期衔接系列答案
初中暑期衔接系列答案 已知点F是抛物线y2=2px的焦点,其中p是正常数,点M的坐标为(12,8),点N在抛物线上,且满足$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$,O为坐标原点.
已知点F是抛物线y2=2px的焦点,其中p是正常数,点M的坐标为(12,8),点N在抛物线上,且满足$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$,O为坐标原点.