题目内容
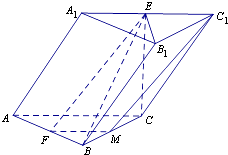
【题目】斜三棱柱A1B1C1﹣ABC中，侧面AA1C1C⊥底面ABC，侧面AA1C1C是菱形，∠A1AC=60°，AC=3，AB=BC=2，E、F分别是A1C1 ， AB的中点． 
（1）求证：EF∥平面BB1C1C；
（2）求证：CE⊥面ABC．
（3）求四棱锥E﹣BCC1B1的体积．
【答案】
（1）证明：取BC中点M，连结FM，C1M．在△ABC中，
∵F，M分别为BA，BC的中点，
∴FM∥AC，FM= 
AC．
∵E为A1C1的中点，AC∥A1C1
∴FM∥EC1且FM=EC1，
∴四边形EFMC1为平行四边形∴EF∥C1M．
∵C1M平面BB1C1C，EF平面BB1C1C，∴EF∥平面BB1C1C
（2）证明：连接A1C，∵四边形AA1C1C是菱形，∠A1AC=60°
∴△A1C1C为等边三角形
∵E是A1C1的中点．∴CE⊥A1C1
∵四边形AA1C1C是菱形，∴A1C1∥AC．∴CE⊥AC．
∵侧面AA1C1C⊥底面ABC，且交线为AC，CE面AA1C1C
∴CE⊥面ABC
（3）连接B1C，∵四边形BCC1B1是平行四边形，所以四棱锥 
= 
由第（2）小问的证明过程可知 EC⊥面ABC
∵斜三棱柱A1B1C1﹣ABC中，∴面ABC∥面A1B1C1．∴EC⊥面EB1C1
∵在直角△CEC1中CC1=3， 
，∴ 
∴ 
∴四棱锥 = =2× 
【解析】（1）通过作平行线，由线线平行证明线面平行即可；（2）根据面面垂直，只需证明CE垂直于交线即可；（3）根据底面积相等，同高的棱锥体积相等，将四棱锥分割为两个体积相等的三棱锥，再根据体积公式求三棱锥的体积即可．
练习册系列答案
相关题目
