题目内容
某几何体的三视图如图所示,当 取最大值时,这个几何体的体积为( )
取最大值时,这个几何体的体积为( )
A. | B. | C.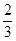 | D.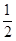 |
D
解析试题分析:该几何体是长方体一角,如图所示,可知AC= ,BD=1,BC=b,AB=a.
,BD=1,BC=b,AB=a.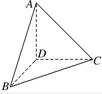
设CD=x,AD=y,
则x2+y2=6,x2+1=b2,y2+1=a2,
消去x2,y2得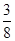 .a2+b2=8≥
.a2+b2=8≥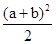 ,所以(a+b)≤4,
,所以(a+b)≤4,
当且仅当a=b=2时等号成立,此时x=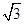 ,y=
,y=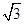 ,
,
所以V=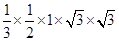 =
=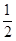 .故选D.
.故选D.
考点:本题主要考查三视图,几何体体积计算,均值定理的应用。
点评:中档题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。本题与均值定理相结合,扩大了试题考查的覆盖面。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是
| A.平行 | B.相交且垂直 | C.异面 | D.相交成60° |
在正方体 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值构成的集合是( )
所成角的正切值构成的集合是( )
A. | B. | C. | D. |
有一个几何体的三视图如图所示,则该几何体的体积为
| A.16 | B.20 | C.24 | D.32 |
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )。
A.4(9+2 ) cm2 ) cm2 | B. cm2 cm2 | C. cm2 cm2 | D. cm cm |
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
A. | B. | C. | D. |












