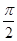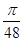题目内容
某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是正三角形)，根据图中标出的数据，可得这个几何体的表面积为（ ）
A． | B． | C． | D．12 |
B
解析试题分析：由三视图可知：该几何体为正四棱锥，其高为4、底面是一个边长为2的正方形，每个侧面是底边为2、高为
的等腰三角形．据此可计算出答案．解：由三视图可知：该几何体为正四棱锥，其高为4、底面是一个边长为2的正方形，每个侧面是底边为2、高为于是这个几何体的表面积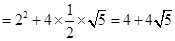
，故答案选B.
考点：三视图还原几何体
点评：由三视图容易知道原几何体是一个正四棱锥，再由画三视图的要求“长对正，高平齐，宽相等”得出数据，算出答案．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A．三点确定一个平面 |
| B．四边形一定是平面图形 |
| C．梯形一定是平面图形 |
D．平面 和平面 有不同在一条直线上的三个交点 |
. 则
的外接圆的面积为
·
=0，沿BD折成直二面角A一BD－C，且4AB2 +2BD2 =1，则三棱锥A－BCD的外接球的表面积为（ ）
某几何体的三视图如下图所示，则该几何体为（ ）
| A．三棱柱 | B．三棱锥 | C．圆锥 | D．四棱锥 |
若
，
是异面直线，，
也是异面直线，则与的位置关系是
| A．异面 | B．相交或平行 | C．平行或异面 | D．相交或平行或异面 |
如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是
| A．平行 | B．相交且垂直 | C．异面 | D．相交成60° |
某三棱锥的三视图如图所示，该三梭锥的表面积是（ ）
A．60+12 | B．56+ 12 |
| C．30+6 | D．28+6 |
在正方体
中，
是棱
的中点，
是侧面
内的动点，且
平面
，则
与平面所成角的正切值构成的集合是（ ）
A． | B． | C． | D． |