题目内容
(本小题满分12分)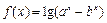 (
(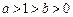 )
)
(1)求 的定义域;
的定义域;
(2)问是否存在实数 、
、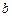 ,当
,当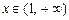 时,
时, 的值域为
的值域为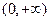 ,且
,且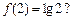 若存在,求出
若存在,求出 、
、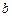 的值,若不存在,说明理由.
的值,若不存在,说明理由.
解:(1)由 得
得 ,
,
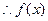 的定义域为
的定义域为
(2)令 ,又
,又 ,
, 上为增函数。
上为增函数。
当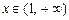 时,
时, 的值取到一切正数等价于
的值取到一切正数等价于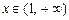 时,
时,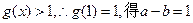 ,① 又
,① 又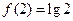 ,
,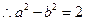 ②
②
由①②得
解析

练习册系列答案
相关题目
函数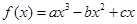 的图象如图所示,且
的图象如图所示,且 在
在 与
与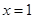 处取得极值,给出下列判断:
处取得极值,给出下列判断: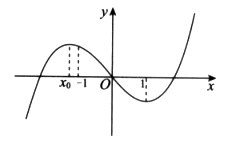
①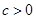 ;
;
②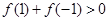 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
 )已知
)已知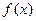 是定义在
是定义在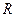 上的奇函数,且
上的奇函数,且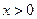 时,
时,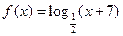 .
.  ,
,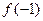
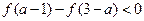 ,求
,求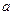 的取值
的取值 范围
范围 的图
的图 象.
象. 时函数的值域
时函数的值域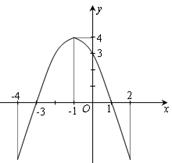
 的反函数为
的反函数为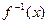 ,
, .
. ,求
,求 的取值范围D;
的取值范围D;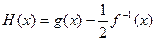 ,当
,当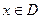 时,求函数
时,求函数 的值域.
的值域. 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: 均有
均有 成立;
成立;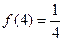 ;
; 时,都有
时,都有 成立。
成立。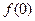 ,
, 的值;
的值; 的不等式
的不等式 .
.