题目内容
函数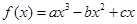 的图象如图所示,且
的图象如图所示,且 在
在 与
与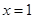 处取得极值,给出下列判断:
处取得极值,给出下列判断: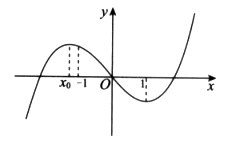
①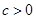 ;
;
②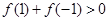 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
C
解析试题分析: ,由图可知
,由图可知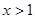 时,
时,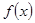 为增函数知
为增函数知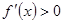 ,所以有
,所以有 。又由
。又由 ,所以有
,所以有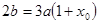 ,
, ,因为
,因为 ,所以
,所以 ,因为
,因为 所以有
所以有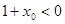 ,所以
,所以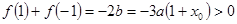 ,
,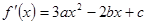 开口向上,对称轴为
开口向上,对称轴为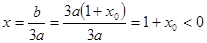 ,所以函数
,所以函数 在区间
在区间 上是是增函数。
上是是增函数。
考点:导数在求函数极值及单调性中的应用

练习册系列答案
相关题目
函数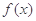 的定义域为开区间
的定义域为开区间 ,导函数
,导函数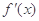 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间 内有极小值点( )
内有极小值点( )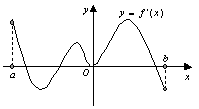
A.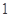 个 个 | B. 个 个 | C.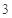 个 个 | D. 个 个 |
已知函数 在区间
在区间 上单调递减,则
上单调递减,则 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
函数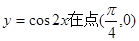 处的切线方程是( )
处的切线方程是( )
A.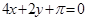 | B.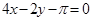 |
C.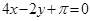 | D.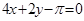 |
设函数f(x)=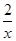 +ln x,则( )
+ln x,则( )
A.x=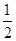 为f(x)的极大值点 为f(x)的极大值点 | B.x=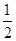 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为f(x)的极大值点 | D.x=2为f(x)的极小值点 |
设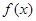 ,
,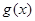 分别是定义在
分别是定义在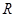 上的奇函数和偶函数,当
上的奇函数和偶函数,当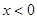 时,
时,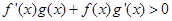 ,且
,且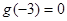 ,则不等式
,则不等式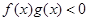 的解集是 ( )
的解集是 ( )
A.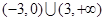 | B.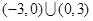 |
C.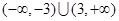 | D.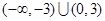 |
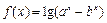 (
(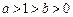 )
) 的定义域;
的定义域; 、
、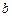 ,当
,当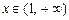 时,
时,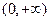 ,且
,且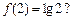 若存在,求出
若存在,求出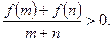
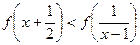 ;
;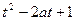 对所有x∈[—1,1],
对所有x∈[—1,1],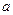 ∈[—1,1]恒成立,求实数t的取值范围.
∈[—1,1]恒成立,求实数t的取值范围. 的图像在点
的图像在点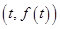 处切线的斜率为
处切线的斜率为 ,则函数
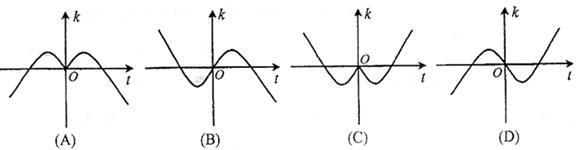
,则函数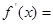
 的部分图像为( )
的部分图像为( )