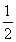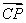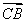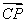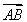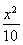题目内容
如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min.在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min，山路AC长为1 260 m，经测量cos A＝
，cos C＝
.
(1)求索道AB的长；
(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？
(3)为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？
（1）1040 m（2）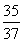
min（3）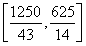
【解析】(1)在△ABC中，因为cos A＝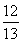
，cos C＝
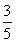，所以sin A＝
，
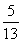sin C＝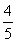
.
从而sin B＝sin[π－(A＋C)]＝sin(A＋C)＝sin Acos C＋cos Asin C＝×＋×＝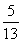
.
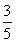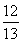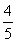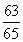由正弦定理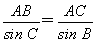
，得AB＝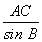
×sin C＝
＝1040(m)．
所以索道AB的长为1040 m.
(2)假设乙出发t分钟后，甲、乙两游客距离为d，此时，甲行走了(100＋50t)m，乙距离A处130t m，所以由余弦定理得d2＝(100＋50t)2＋(130t)2－2×130t×(100＋50t)×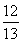＝200(37t2－70t＋50)，因0≤t≤
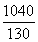，即0≤t≤8，故当t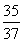＝ (min)时，甲、乙两游客距离最短．
(3)由正弦定理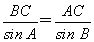
，得BC＝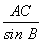
×sin A＝
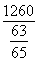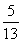×＝500(m)．
乙从B出发时，甲已走了50×(2＋8＋1)＝550(m)，还需走710 m才能到达C.
设乙步行的速度为v m/min，由题意得－3≤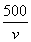
－
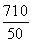≤3，解得
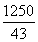≤v≤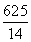
，所以为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在 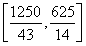(单位：m/min)范围内
