题目内容
6.椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由椭圆方程求出a2,b2的值,代入a2=b2+c2求出c,代入离心率公式求出离心率e的值.
解答 解:由题意知,$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,
∴a2=16,b2=12,则c2=a2-b2=4,
即a=4,c=2,
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,
故选:B.
点评 本题考查椭圆的标准方程以及简单的几何性质,以及椭圆基本量的求法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.一个多面体的三视图如图所示,则该多面体的体积为( )
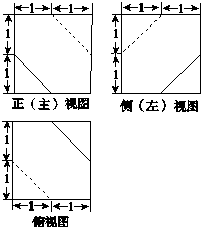

| A. | $\frac{23}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{47}{6}$ | D. | 7 |
1.某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率;
(Ⅲ)若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$,停车付费多于14元的概率为$\frac{5}{12}$,求甲停车付费恰为6元的概率.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
| 甲停车时长 (小时) | (0,1] | (1,2] | (2,3] | (3,4] |
| 甲停车费a (元) |
(Ⅲ)若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$,停车付费多于14元的概率为$\frac{5}{12}$,求甲停车付费恰为6元的概率.
11.下列命题中,正确的是( )
| A. | 如果直线a∥b,那么a平行于经过b的任何平面 | |
| B. | 如果直线a,b和平面α满足a∥α,b∥α,那么a∥b | |
| C. | 如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
18.已知函数f(x)=-x2+ax-b,若a,b都是从区间[0,3]任取的一个数,则f(1)>0成立的概率是( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{8}{9}$ |
15.函数y=sin(x-$\frac{π}{4}$)cos(x-$\frac{π}{4}$)是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |