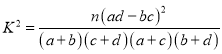题目内容
【题目】函数![]() .
.
(1)根据![]() 不同取值,讨论函数
不同取值,讨论函数![]() 的奇偶性;
的奇偶性;
(2)若![]() ,对于任意的
,对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若已知![]() ,
,![]() . 设函数
. 设函数![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,结合奇偶性的定义得出函数
两种情况讨论,结合奇偶性的定义得出函数![]() 的奇偶性;
的奇偶性;
(2)![]() 满足不等式
满足不等式![]() ,在
,在![]() 时,可得出
时,可得出![]() ,可得出不等式
,可得出不等式![]() 对任意的
对任意的![]() 恒成立,然后利用参变量分离法得出
恒成立,然后利用参变量分离法得出![]() ,利用函数单调性分别求出函数
,利用函数单调性分别求出函数![]() 和
和![]() 在区间
在区间![]() 上的最大值和最小值,即可得出实数
上的最大值和最小值,即可得出实数![]() 的取值范围;
的取值范围;
(3)由题意知,当![]() 时,
时,![]() ,将
,将![]() 代入函数
代入函数![]() 的解析式,求出该函数的最小值,利用复合函数法求出函数
的解析式,求出该函数的最小值,利用复合函数法求出函数![]() 在区间
在区间![]() 上的最大值,然后解不等式
上的最大值,然后解不等式![]() ,即可得出实数
,即可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,关于原点对称.
,关于原点对称.
当![]() 时,
时,![]() ,
,![]() ,
,
此时,函数![]() 为奇函数;
为奇函数;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,此时,函数
,此时,函数![]() 为非奇非偶函数;
为非奇非偶函数;
(2)当![]() 时,则有
时,则有![]() 恒成立,此时
恒成立,此时![]() ;
;
当![]() 时,由
时,由![]() ,即
,即![]() ,即
,即![]() ,
,
![]() ,
,![]() ,则
,则![]() ,所以,不等式
,所以,不等式![]() 对任意的
对任意的![]() 恒成立,
恒成立,
由![]() ,即
,即![]() ,
,![]() ,即
,即![]() .
.
![]() 函数
函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,
,
函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)由题意知,当![]() 时,
时,![]() ,
,
当![]() 时,
时,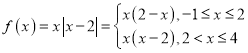 .
.
当![]() 时,
时,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
且![]() ,
,![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() .
.
所以,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
对于函数![]() ,
,
内层函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
外层函数![]() 是减函数,
是减函数,
所以,![]() ,
,
由题意得![]() ,则有
,则有![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|