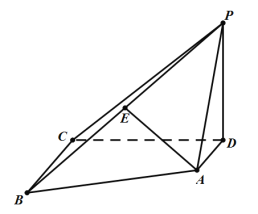
题目内容
【题目】如图所示,在四棱锥![]() 中,
中,![]() 是正三角形,四边形
是正三角形,四边形![]() 为直角梯形,点
为直角梯形,点![]() 为
为![]() 中点,且
中点,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
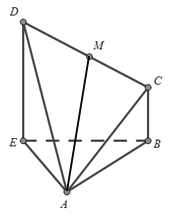
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,并连接
,并连接![]() ,先得出
,先得出![]() 为二面角
为二面角![]() 的平面角,进而得到
的平面角,进而得到![]() ,即可得平面
,即可得平面![]() 平面
平面![]() ;
;
(2)以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量的夹角公式求出两个法向量夹角的余弦值,进而可得二面角
的法向量,利用向量的夹角公式求出两个法向量夹角的余弦值,进而可得二面角![]() 的余弦值.
的余弦值.
(1)证:取![]() 的中点
的中点![]() ,并连接
,并连接![]() .
.
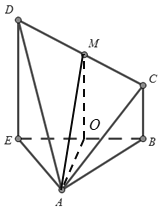
则据题意可得:
中位线![]() 的长为
的长为![]() ,
,
且![]()
又因为![]() 是正三角形,所以
是正三角形,所以![]()
故:![]() 为二面角
为二面角![]() 的平面角
的平面角
而![]() ,
,![]()
有![]() ,即
,即![]()
由定义可知:平面![]() 平面
平面![]()
(2)解:由(1)可得:![]() 平面
平面![]() ,
,![]()
以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
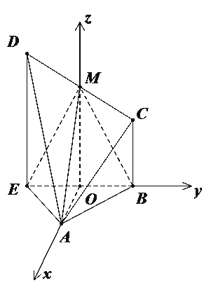
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则有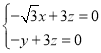
令![]() 可得
可得![]() ;同理可得:
;同理可得:![]() 平面
平面![]()
![]()
![]()
故:二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)为了解该种蛋糕的市场需求情况与性別是否有关,随机统计了100人的购买情况,得如下列联表:
男 | 女 | 合计 | |
购买 | 15 | 35 | 50 |
不购买 | 6 | 44 | 50 |
合计 | 21 | 79 | 100 |
问:能否有![]() 的把握认为是否购买蛋糕与性別有关?
的把握认为是否购买蛋糕与性別有关?
附: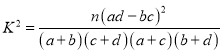
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |