题目内容
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
,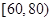 ,
,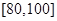 .
.
(1)求直方图中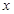 的值;
的值;
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于 分钟的新生,其中2人上学路上时间小于
分钟的新生,其中2人上学路上时间小于 分钟. 从这6人中任选2人,设这2人中上学路上时间小于
分钟. 从这6人中任选2人,设这2人中上学路上时间小于 分钟人数为
分钟人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1)0.025 (2)120 (3)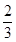
解析试题分析:
(1)根据频率分布直方图可以得到组距,而频率分布直方图的纵坐标与组距之积为频率,各组频率之和为1即可得到x的值.
(2)根据频率分布直方图求出上学路上所需时间不少于60分钟的学生的频率,频率乘以总人数即可得到可以留宿学生的人数.
(3)根据题意可得X的取值为0,1,2,首先利用组合数计算6选2人无序的基本事件数,再利用组合数求的X分别为0,1,2,时的基本事件数,根据古典概型的概率计算公式即可得到相应的概率,从而得到分布列,X的值与对应的概率乘积之和即为期望.
试题解析:
(1)由直方图可得: .
.
所以  . 2分
. 2分
(2)新生上学所需时间不少于60分钟的频率为: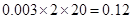 4分
4分
因为
所以 名新生中有
名新生中有 名学生可以申请住宿. 6分
名学生可以申请住宿. 6分
(3) 的可能取值为0,1,2. 7分
的可能取值为0,1,2. 7分
所以 的可能取值为
的可能取值为 7分
7分


所以 的分布列为:
的分布列为:
11分
0[来源:学|科|网] 1 2 



 12分
12分
考点:古典概型 频率分布直方图 频率 分布列 期望

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案一汽车厂生产 、
、 、
、 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车 | 轿车 | 轿车 |
| 舒适型 |  |  |  |
| 标准型 |  |  |  |
 辆,其中有
辆,其中有 类轿车
类轿车 辆.
辆.(1)求
 的值;
的值;(2)用分层抽样的方法在
 类轿车中抽取一个容量为
类轿车中抽取一个容量为 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取 辆,求至少有
辆,求至少有 辆舒适型轿车的概率;
辆舒适型轿车的概率;(3)用随机抽样的方法从
 类舒适型轿车中抽取
类舒适型轿车中抽取 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .把这
.把这 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过
 的概率.
的概率. 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1) 求图中a的值;
(2) 根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3) 若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
某电视台举办青年歌手大奖赛,有10名评委打分,已知甲、乙两名选手演唱后的打分情况如茎叶图所示:
| 甲 | | 乙 |
| 6 4 3 | 9 | 1 5 |
| 8 7 7 5 4 2 | 8 | 0 1 3 6 6 8 8 9 |
| 9 | 7 | |
(2)现场有3名点评嘉宾A、B、C,每位选手可以从中选2位进行指导,若选手选每位点评嘉宾的可能性相等,求甲乙两选手选择的点评嘉宾恰重复一人的概率.
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | | |
| 合计 | 50 | |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…799, 试写出第二组第一位学生的编号;
(2)填充频率分布表的空格(将答案直接填在表格内) ,并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的约多少人?

 ;
; 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 )的概率;
)的概率; 的数学期望.
的数学期望.
 ≈5.059)
≈5.059)