题目内容
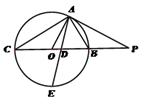
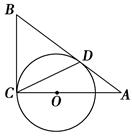
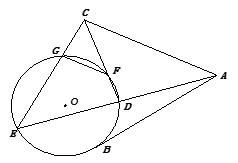
如图所示, 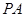 为圆
为圆 的切线,
的切线,  为切点,
为切点,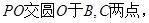
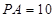 ,
,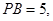
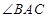 的角平分线与
的角平分线与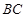 和圆
和圆 分别交于点
分别交于点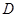 和
和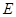 .
.
(1)求证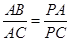 (2)求
(2)求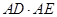 的值.
的值.
(1)证明过程详见解析;(2) .
.
解析试题分析:本题以圆为几何背景考查线和线的关系以及相似三角形的证明,考查学生的转化和化归能力.第一问,利用已知证明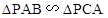 ,所以通过相似三角形的性质得
,所以通过相似三角形的性质得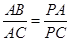 ;第二问,先利用圆的切割线定理得
;第二问,先利用圆的切割线定理得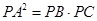 ,所以得
,所以得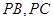 的长,在
的长,在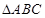 中利用勾股定理求出
中利用勾股定理求出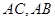 的长,通过上述条件证明
的长,通过上述条件证明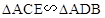 ,得到
,得到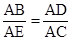 ,所以得出
,所以得出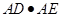 的值.
的值.
试题解析:(1)∵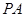 为圆
为圆 的切线,
的切线, 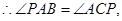 又
又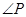 为公共角,
为公共角,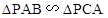
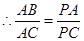 4分
4分
(2)∵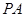 为圆
为圆 的切线,
的切线,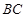 是过点
是过点 的割线,
的割线, 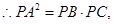
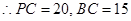
又∵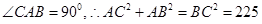
又由(1)知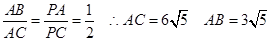 ,连接
,连接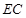 ,则
,则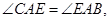
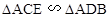 ,
,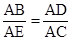
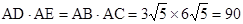 .10分
.10分
考点:1.三角形相似;2.勾股定理;3.切割线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

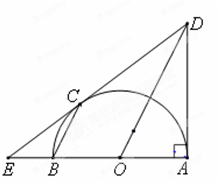
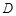 为锐角
为锐角 的内切圆圆心,过点
的内切圆圆心,过点 作直线
作直线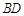 的垂线,垂足为
的垂线,垂足为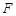 ,圆
,圆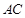 相切于点
相切于点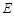 .若
.若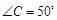 ,求
,求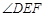 的度数.
的度数.
 是
是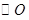 的一条切线,切点为
的一条切线,切点为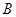 ,
,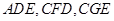 都是
都是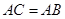 .
.
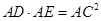 ;
;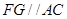 .
.
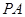 与圆
与圆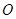 相切于点
相切于点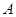 ,直径
,直径 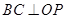 ,连结
,连结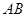 交
交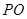 于点
于点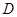 .
.
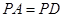 ;
;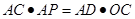 .
.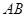 过圆心
过圆心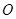 ,交⊙
,交⊙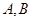 ,直线
,直线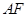 交⊙
交⊙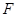 (不与
(不与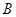 重合),直线
重合),直线 与⊙
与⊙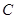 ,交
,交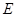 ,且与
,且与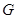 ,连结
,连结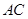 .
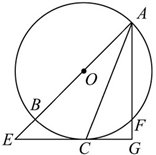
.
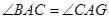 ;
; 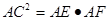 .
.