题目内容
13．已知x，y满足线性规划$\left\{\begin{array}{l}{x+y-4＜0}\\{y-x＞0}\\{2x+y-4＞0}\end{array}\right.$，则x2+y2-6x-4y+14的取值范围是（ ）| A． | [2，14] | B． | （2，14） | C． | [2，$\sqrt{13}$+1] | D． | （2，$\sqrt{13}$+1） |
分析 由题意作出其平面区域，（x-3）2+（y-2）2可看成阴影内的点到点C（3，2）的距离的平方，求阴影内的点到C（3，2）的距离的范围可得．
解答 解：由题意作出其平面区域，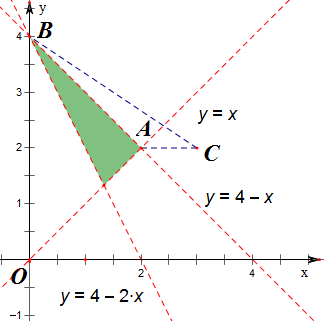
x2+y2-6x-4y+14=（x-3）2+（y-2）2+1，
（x-3）2+（y-2）2可看成阴影内的点到点C（3，2）的距离的平方，又A（2，2），B（0，4）；
故（2-3）2+（2-2）2＜（x-3）2+（y-2）2＜（0-3）2+（4-2）2，
即1＜（x-3）2+（y-2）2＜13，
故2＜（x-3）2+（y-2）2+1＜14，
故选：B．
点评 本题考查了简单线性规划，作图要细致认真，用到了表达式的几何意义的转化，属于中档题．
练习册系列答案
习题精选系列答案
相关题目
如图，在直三棱柱ABC-A1B1C1中，AA1=$\sqrt{3}$，△ABC是正三角形，P是棱A1C1的中点．
18．
如图是某篮球联赛中，甲、乙两名运动员9个场次得分的茎叶图，设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$，中位数分别为m甲，m乙，则（ ）
如图是某篮球联赛中，甲、乙两名运动员9个场次得分的茎叶图，设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$，中位数分别为m甲，m乙，则（ ）| A． | ${\overline{x}}_{甲}$＜${\overline{x}}_{乙}$，m甲＜m乙 | B． | ${\overline{x}}_{甲}$＜${\overline{x}}_{乙}$，m甲＞m乙 | ||
| C． | ${\overline{x}}_{甲}$＞${\overline{x}}_{乙}$，m甲＞m乙 | D． | ${\overline{x}}_{甲}$＞${\overline{x}}_{乙}$，m甲＜m乙 |
2．与圆（x-2）2+y2=1外切，且与y轴相切的动圆圆心P的轨迹方程为（ ）
| A． | y2=6x-3 | B． | y2=2x-3 | C． | x2=6y-3 | D． | x2-4x-2y+3=0 |