题目内容
18．已知中心在原点且经过点（2，1）的椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），试求a的取值范围．分析 由点（2，1）在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上，可得$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1，从而可求a的取值范围．
解答 解：∵点（2，1）在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上，
∴$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1，
即$\frac{4}{{a}^{2}}$=1-$\frac{1}{{b}^{2}}$＞0，
∴b2＞1．
又b＜$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴1＜b2＜5．
a2=$\frac{4{b}^{2}}{{b}^{2}-1}$=$\frac{4}{{b}^{2}-1}$+4＞4+1=5，
∴a＞$\sqrt{5}$
即a的取值范围为（$\sqrt{5}$，+∞）．
点评 本题考查椭圆方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
6．如果y=f（x）的反函数是y=f-1（x），则下列命题中一定正确的是（ ）
| A． | 若y=f（x）在[1，2]上是增函数，则y=f-1（x）在[1，2]上也是增函数 | |
| B． | 若y=f（x）是奇函数，则y=f-1（x）也是奇函数 | |
| C． | 若y=f（x）是偶函数，则y=f-1（x）也是偶函数 | |
| D． | 若y=f（x）的图象与y轴有交点，则y=f-1（x）的图象与y轴也有交点 |
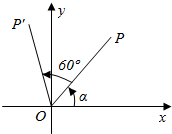如图，保持点P（3，3）与原点的距离不变，并绕原点旋转60°到P′位置，设点P′的坐标为（x′，y′）．