题目内容
8．若直线l沿x轴向左平移3个单位，再向下平移2个单位后，回到原来的位置，则直线l的斜率为$\frac{2}{3}$．分析 设直线l的方程为：y=kx+b，利用平移变换的规则：“左加右减，上加下减”，求出变换后直线方程，再由条件求出直线的斜率．
解答 解：设直线l的方程为：y=kx+b，
∵直线l沿x轴向左平移3个单位，再沿y轴向下平移2个单位后，
∴变换后的直线方程是：y=kx+3k+b-2．
∵经过两次平移变换后回到原来的位置，
∴必有3k+b-2=b，解得k=$\frac{2}{3}$，
故答案为．$\frac{2}{3}$
点评 本题考查图象的变换，熟练掌握平移变换的规律是解题关键，属于基础题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
16．已知直线y=k（x+a）（a＞0）与x轴交于点A，与直线x=c（c＞0，c＜a）交于点M，椭圆C以A为左顶点，以F（c，0）为右焦点，且过点M，当$\frac{1}{3}$＜k＜$\frac{1}{2}$时，椭圆C的离心率的范围是（ ）
| A． | $（0，\frac{2}{3}）$ | B． | $（\frac{2}{3}，1）$ | C． | $（\frac{1}{2}，1）$ | D． | $（\frac{1}{2}，\frac{2}{3}）$ |
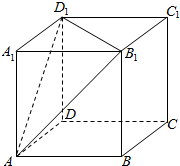如图所示，正方体ABCD-A1B1C1D1的棱长为6，则以正方体ABCD-A1B1C1D1的中心为顶点，以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$．