题目内容
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.
(1)直线 与
与 不能垂直;(2)
不能垂直;(2)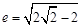
解析试题分析:(1)设直线 的方程为
的方程为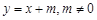 ,与椭圆方程联立,消去
,与椭圆方程联立,消去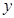 整理为关于
整理为关于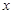 的一元二次方程,因为有两个交点则判别式应大于0,由韦达定理可得根与系数的关系,用中点坐标公式求点
的一元二次方程,因为有两个交点则判别式应大于0,由韦达定理可得根与系数的关系,用中点坐标公式求点 的坐标。求出直线
的坐标。求出直线 的斜率,假设两直线垂直则斜率相乘等于
的斜率,假设两直线垂直则斜率相乘等于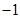 ,解出
,解出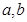 的关系式,根据关系式及椭圆中
的关系式,根据关系式及椭圆中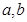 的关系判断假设成立与否。(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
的关系判断假设成立与否。(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
∵ ,∴四边形OANB为矩形,∴
,∴四边形OANB为矩形,∴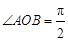 ,转化为向量问题,可得
,转化为向量问题,可得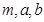 的关系式。由中点坐标公式可得点
的关系式。由中点坐标公式可得点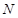 的坐标,将其代入椭圆方程,与上式联立消去
的坐标,将其代入椭圆方程,与上式联立消去 即可得
即可得 之间满足的关系式。将
之间满足的关系式。将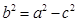 代入
代入 之间的关系式,可求其离心率。
之间的关系式,可求其离心率。
试题解析:解答:(1)∵斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点,
∴可以设直线 的方程为
的方程为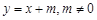 .
.
∵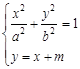 ,∴
,∴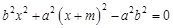 ,
,
∴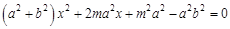 . ① 1分
. ① 1分
∵直线 与椭圆相交于
与椭圆相交于 两点,∴
两点,∴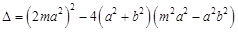
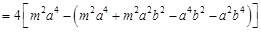
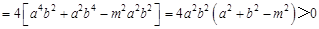 . ② 2分
. ② 2分
且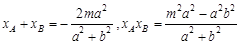 . ③ 3分
. ③ 3分
∵ 为线段
为线段 的中点,∴
的中点,∴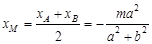 ,
,
∴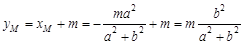 ,∴
,∴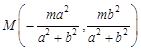 . 4分
. 4分
假设直线 与
与 能垂直.
能垂直.
∵直线 的斜率为1,∴直线
的斜率为1,∴直线 的斜率为-1,
的斜率为-1,
∴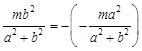 ,∴
,∴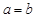 . 5分
. 5分
∵在椭圆方程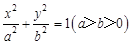 中,
中,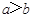 ,
,
∴假设不正确,在椭圆中直线 与
与 不能垂直. 6分
不能垂直. 6分
(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
∵ ,∴四边形OANB为矩形,∴
,∴四边形OANB为矩形,∴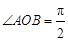 , 7分
, 7分
∴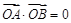 ,∴
,∴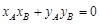 ,∴
,∴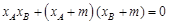 ,
,
∴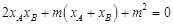 ,
,
∴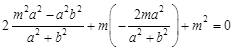 ,整理得
,整理得 . 8分
. 8分
∵ 点在椭圆上,∴
点在椭圆上,∴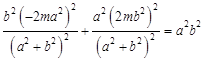 ,∴
,∴ . 9分
. 9分
此时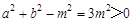 ,满足
,满足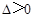 ,
,
消去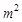 得
得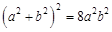 ,即
,即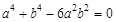 . 10分
. 10分
设椭圆的离心率为e,则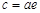 ,∴
,∴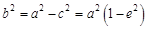 ,
,
∴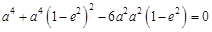 ,∴
,∴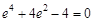 ,
,
∴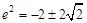 ,∵
,∵
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 ,线段
,线段 垂直平分线交
垂直平分线交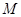 ,求点
,求点 的方程;
的方程; 轴交于点
轴交于点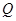 ,不同的两点
,不同的两点 在
在 ,求
,求 的取值范围.
的取值范围.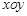 中,动点
中,动点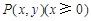 满足:点
满足:点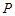 到定点
到定点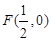 与到
与到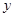 轴的距离之差为
轴的距离之差为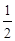 .记动点
.记动点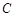 .
.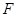 的直线交曲线
的直线交曲线 、
、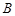 两点,过点
两点,过点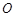 的直线交直线
的直线交直线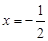 于点
于点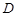 ,求证:直线
,求证:直线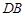 平行于
平行于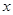 轴.
轴.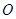 ,焦点
,焦点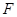 在
在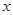 轴上,抛物线上的点
轴上,抛物线上的点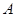 到
到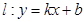 与抛物线交于
与抛物线交于 ,
, 两点.
两点.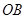 ,
,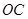 的倾斜角之和为
的倾斜角之和为 时,证明直线
时,证明直线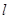 过定点.
过定点. 经过
经过 、
、 两点
两点  交双曲线
交双曲线 、
、 两点,且线段
两点,且线段 被圆
被圆 :
: 三等分,求实数
三等分,求实数 、
、 的值
的值 
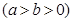 的离心率为
的离心率为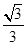 ,直线
,直线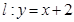 与圆
与圆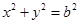 相切.
相切.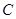 的方程;
的方程;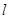 与椭圆
与椭圆 ,求弦长
,求弦长 .
.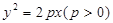 ,其准线方程为
,其准线方程为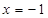 ,过准线与
,过准线与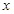 轴的交点
轴的交点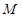 做直线
做直线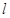 交抛物线于
交抛物线于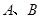 两点.
两点.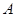 为
为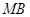 中点,求直线
中点,求直线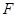 ,当
,当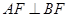 时,求
时,求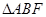 的面积.
的面积.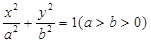 上的点
上的点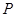 到左右两焦点
到左右两焦点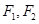 的距离之和为
的距离之和为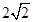 ,离心率为
,离心率为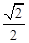 .
.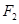 的直线
的直线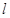 交椭圆于
交椭圆于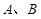 两点,若
两点,若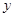 轴上一点
轴上一点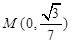 满足
满足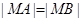 ,求直线
,求直线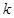 的值.
的值.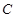 两焦点坐标分别为
两焦点坐标分别为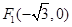 ,
,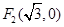 ,且经过点
,且经过点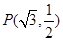 .
.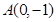 ,直线
,直线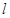 与椭圆
与椭圆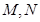 .若△
.若△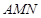 是以
是以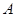 为直角顶点的等腰直角三角形,试求直线
为直角顶点的等腰直角三角形,试求直线