题目内容
6．已知函数$f（x）=\left\{\begin{array}{l}|{log_3}x|，0＜x≤3\\{（x-4）^2}，x＞3\end{array}\right.$，若方程f（x）=m有四个不同的实数根，由小到大依次为x1，x2，x3，x4，则4x1+x2+x3+x4的取值范围是[12，13）．分析 作函数$f（x）=\left\{\begin{array}{l}|{log_3}x|，0＜x≤3\\{（x-4）^2}，x＞3\end{array}\right.$的图象，从而可得x1x2=1，x3+x4=8；从而由基本不等式确定的取值范围．
解答 解：作函数$f（x）=\left\{\begin{array}{l}|{log_3}x|，0＜x≤3\\{（x-4）^2}，x＞3\end{array}\right.$的图象如下，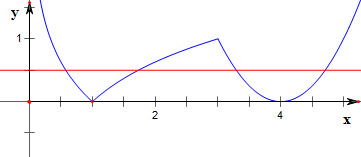
由题意知，
x1x2=1，x3+x4=8；
4x1+x2≥2$\sqrt{4}$=4，
（当且仅当4x1=x2，即4x1=x2=2时，等号成立）；
故4x1+x2+x3+x4≥12，
且4x1+x2+x3+x4＜13；
故答案为：[12，13）．
点评 本题考查了分段函数的应用及基本不等式的应用，属于中档题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
（1）设实数x，y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$，作出不等式组表示的平面区域，并求当a＞0时，z=y-ax的最大值；
18．设X为随机变量，X～B （n，$\frac{1}{3}$），若随机变量X的数学期望E（X）=2，则P（X=2）等于（ ）
| A． | $\frac{80}{243}$ | B． | $\frac{13}{243}$ | C． | $\frac{4}{243}$ | D． | $\frac{13}{16}$ |
15．如图是某三棱锥的三视图，则该三棱锥的表面积为（ ）
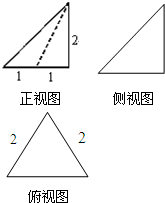
| A． | 4+$\sqrt{7}+\sqrt{3}$ | B． | 6+$\sqrt{7}$ | C． | 4+$\sqrt{7}$ | D． | 6+$\sqrt{3}$ |