题目内容
1.下列函数中,在x=0处的导数不等于零的是( )| A. | y=x-ex | B. | y=x2•ex | C. | y=x(1-x) | D. | y=x3+x2 |
分析 分别求出四个答案的导数,把x=0代入即可得到答案.
解答 解:A选项y=x-ex的导函数y′=1-ex,令x=0得到y′=0;
B选项y=x2•ex的导函数y′=2xex+x2•ex,令x=0得到y′=0;
C选项y=x(1-x)的导函数y′=-2x+1,令x=0得到y′=1;
D选项y=x3+x2的导函数y′=3x2+2x,令x=0得到y′=0.
故选:C.
点评 本题考查了导数的运算法则,关键是掌握基本导数公式,属于基础题.

练习册系列答案
相关题目
6.定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f($\frac{x}{5}$)=$\frac{1}{2}f(x)$,且当0≤x1≤x2≤1时,f(x1)≤f(x2),则f($\frac{1}{2015}$)等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
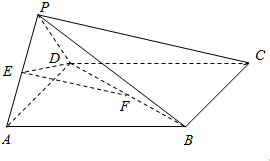 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°. 在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.
在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.