Question

【题目】为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1 km内不能收到手机信号．检查员抽查青岛市一考点，在考点正西约 km有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以12 km/h的速度沿公路行驶，最长需要多少时间，检查员开始收不到信号，并至少持续多长时间该考点才算合格？

Answer 1

【答案】最长需要5 min检查员开始收不到信号，并至少持续5 min该考点才算合格

【解析】试题分析：根据题意，设公路上两点到考点的距离为，在中根据正弦定理计算出，从而得到，进而得到是边长为的等边三角形，得到，再由检查员的行驶速度和长，即可算出各自需要的时间。

解析：如图所示，考点为A，检查开始处为B，设公路上C，D两点到考点的距离为1 km．

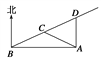
在△ABC中，AB＝≈1．732，AC＝1，∠ABC＝30°，

由正弦定理，得sin∠ACB＝＝，

∴∠ACB＝120°(∠ACB＝60°不合题意)，

∴∠BAC＝30°，∴BC＝AC＝1．

在△ACD中，AC＝AD，∠ACD＝60°，

∴△ACD为等边三角形，∴CD＝1．

∵×60＝5，

∴在BC上需要5 min，CD上需要5 min．

∴最长需要5 min检查员开始收不到信号，并至少持续5 min该考点才算合格．