题目内容
【题目】已知椭圆C的两个焦点是F1（﹣2，0），F2（2，0），且椭圆C经过点A（0， 
）．
（1）求椭圆C的标准方程；
（2）若过椭圆C的左焦点F1（﹣2，0）且斜率为1的直线l与椭圆C交于P、Q两点，求线段PQ的长（提示：|PQ|= 
|x1﹣x2|）．
【答案】
（1）解：由题意可知椭圆焦点在x轴上，设椭圆方程为 
（a＞b＞0），
由题意可知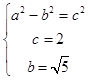 
，∴a=3，b= 
．
∴椭圆的标准方程为 
=1
（2）解：直线l的方程为y=x+2，
联立方程组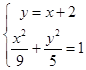 
，得14x2+36x﹣9=0，
设P（x1，y1），Q（x2，y2），则x1+x2=﹣ 
，x1x2=﹣ 
，
∴|PQ|= 
|x1﹣x2|= 
= 
= 
【解析】（1）利用待定系数法求出椭圆方程；（2）联立方程组，利用根与系数的关系和弦长公式计算弦长．
【题目】下面（A）（B）（C）（D）为四个平面图形： 
（1）数出每个平面图形的交点数、边数、区域数，并将下表补充完整：
交点数 | 边数 | 区域数 | |
（A） | 4 | 5 | 2 |
（B） | 5 | 8 | |
（C） | 12 | 5 | |
（D） | 15 |
（2）观察表格，若记一个平面图形的交点数、边数、区域数分别为E、F、G，试猜想E、F、G之间的数量关系（不要求证明）．
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
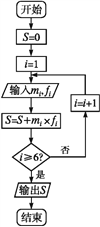
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
