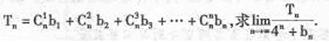题目内容
已知各项都是正数的等比数列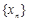 ,满足
,满足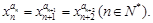
(I)证明数列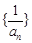 是等差数列;
是等差数列;
(II)若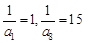 ,当
,当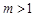 时, 不等式
时, 不等式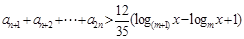 对
对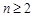 的正整数恒成立,求
的正整数恒成立,求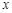 的取值范围.
的取值范围.
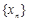 ,满足
,满足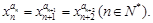
(I)证明数列
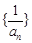 是等差数列;
是等差数列;(II)若
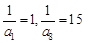 ,当
,当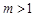 时, 不等式
时, 不等式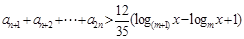 对
对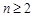 的正整数恒成立,求
的正整数恒成立,求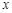 的取值范围.
的取值范围.
(II)由(Ⅰ)设
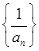 的公差为
的公差为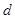 ,知
,知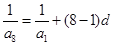 ,
,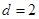 ,
,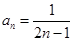 ,
,令
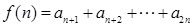 ,则
,则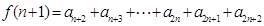 ,
,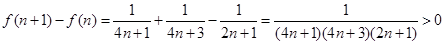 .
.…(8分)
∴函数
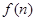 单调递增, 当
单调递增, 当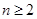 时,
时,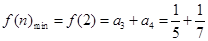 .
.∴
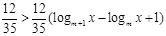 ,即
,即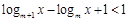 , …………(10分)
, …………(10分)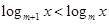 ,
,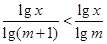 ,
,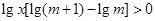 .
.而
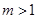 ,∴
,∴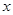 的取值范围是
的取值范围是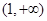 .
. 略

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0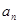 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论 中,
中,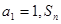 是数列
是数列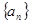 的前
的前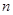 项和,对任意
项和,对任意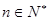 ,有
,有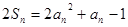 .函数
.函数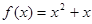 ,数列
,数列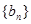 的首项
的首项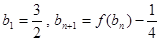
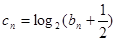 求证:
求证: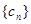 是等比数列并求
是等比数列并求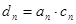 ,
, ,求数列
,求数列 的前n项和
的前n项和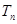 .
.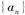 的前n项和为
的前n项和为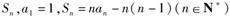 .
.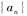 的通项公式;
的通项公式;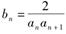 ,求数列
,求数列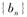 的前n项和Tn
的前n项和Tn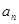 }满足
}满足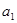 =1,
=1,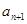 =
=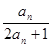 ,(1)计算
,(1)计算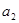 ,
,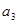 ,
,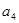 的值;
的值;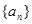 是等比数列,首项
是等比数列,首项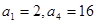 .
.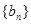 是等差数列,且
是等差数列,且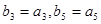 求数列
求数列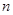 项和
项和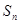 .
. 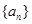 、
、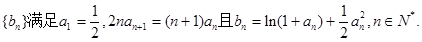
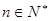 ,证明:
,证明: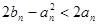 成立;
成立;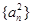 、
、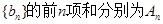 、
、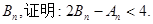
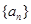 中,
中,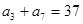 ,则
,则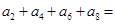 __________。
__________。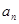 }为等差数列,公差d≠0,同{
}为等差数列,公差d≠0,同{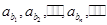 为等比数列,其中
为等比数列,其中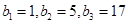 。
。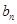 }的通项公式;
}的通项公式;